
已知 、
、 、
、 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中
(1)若 ,且
,且 ,求
,求 的坐标;
的坐标;
(2)若 ,且
,且 与
与 垂直,求
垂直,求 与
与 的夹角
的夹角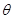 .
.
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
已知 为坐标原点,
为坐标原点, =(
=( ),
), =(1,
=(1, ),
),  .
.
(1)若 的定义域为[-
的定义域为[- ,
, ],求y=
],求y= 的单调递增区间;
的单调递增区间;
(2)若 的定义域为[
的定义域为[ ,
, ],值域为[2,5],求
],值域为[2,5],求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知 =(cosα,sinα),
=(cosα,sinα), =(cosβ,sinβ),
=(cosβ,sinβ), 与
与 之间有关系|k
之间有关系|k +
+ |=
|= |
| -k
-k |,其中k>0,(Ⅰ)用k表示
|,其中k>0,(Ⅰ)用k表示 ;
;
(Ⅱ)求 ·
· 的最小值,并求此时
的最小值,并求此时 与
与 的夹角的大小。
的夹角的大小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com