
【题目】如图所示,已知直线![]() 与双曲线
与双曲线![]() 交于A,B两点,且点A的横坐标为4.
交于A,B两点,且点A的横坐标为4.
(1)求![]() 的值及B点坐标;
的值及B点坐标;
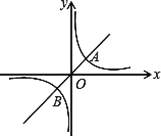
(2)结合图形,直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.
科目:高中数学 来源: 题型:
【题目】农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况,从甲、乙两种麦苗的试验田中各抽取6株麦苗测量麦苗的株高,数据如下:(单位:cm)
甲:9,10,11,12,10,20
乙:8,14,13,10,12,21.
(1)在给出的方框内绘出所抽取的甲、乙两种麦苗株高的茎叶图;
(2)分别计算所抽取的甲、乙两种麦苗株高的平均数与方差,并由此判断甲、乙两种麦苗的长势情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
: ![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
, ![]() 两点,记抛物线在
两点,记抛物线在![]() ,
, ![]() 两点处的切线
两点处的切线![]() ,
, ![]() 的交点为
的交点为![]() .
.
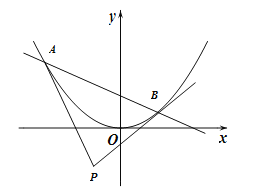
(I)求证: ![]() ;
;
(II)求点![]() 的坐标(用
的坐标(用![]() ,
, ![]() 表示);
表示);
(Ⅲ)若![]() ,求△
,求△![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,PD⊥底面ABCD,AD∥BC,AC⊥DB,∠CAD=60°,AD=2,PD=1.
(1)证明:AC⊥BP;
(2)求二面角C﹣AP﹣D的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内圆心为![]() 的圆的方程为
的圆的方程为![]() ,点
,点![]() 是圆上的动点,点
是圆上的动点,点![]() 是平面内任意一点,若线段
是平面内任意一点,若线段![]() 的垂直平分线交直线
的垂直平分线交直线![]() 于点
于点![]() ,则点
,则点![]() 的轨迹可能是_________.(请将下列符合条件的序号都填入横线上)
的轨迹可能是_________.(请将下列符合条件的序号都填入横线上)
①椭圆;②双曲线;③抛物线;④圆;⑤直线;⑥一个点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三年级期中考试的学生中随机统计了40名学生的政治成绩,这40名学生的成绩全部在40分至100分之间,据此绘制了如图所示的样本频率分布直方图.

(1)求成绩在[80,90)的学生人数;
(2)从成绩大于等于80分的学生中随机选2名学生,求至少有1 名学生成绩在[90,100]的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将号码分别为1、2、…、9的九个小球放入一个袋中,这些小球仅号码不同,其余完全相同,甲从袋中摸出一个球.其号码为a,放回后,乙从此袋中再摸出一个球,其号码为b,则使不等式a-2b+10>0成立的事件发生的概率等于________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]()
(1)讨论![]() 的单调区间和极值;
的单调区间和极值;
(2)将函数![]() 的图象向下平移1个单位后得到
的图象向下平移1个单位后得到![]() 的图象,且
的图象,且![]() 为自然对数的底数)和
为自然对数的底数)和![]() 是函数
是函数![]() 的两个不同的零点,求
的两个不同的零点,求![]() 的值并证明:
的值并证明: ![]() 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com