
分析 本题的关键是理解点A(x,y)实施变换f后,对应点为A1(y,x)这一变换过程,针对每一个方程给出变换后的正确方程.
解答 解:①圆x2+y2=r2(r≠0)上任意一点实施变换f后,
显然互换x,y后,对应点的轨迹仍是圆x2+y2=r2(r≠0);
则①正确;
②若直线y=kx+b上每一点实施变换f后,
互换x,y后,对应点的轨迹方程:x=ky+b,若应点的轨迹方程仍是y=kx+b,
那么k=±1且b=0,则②不正确;
③椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上每一点实施变换f后,
对应点的轨迹:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0),
那么对应点的轨迹仍是离心率不变的椭圆,则③正确;
④曲线C:y=-x2+2x-1(x>0)上每一点实施变换f后,
对应点的轨迹是曲线C1:x=-y2+2y-1(x>0)
将y=x向下平移$\frac{3}{4}$个单位得到直线y=x-$\frac{3}{4}$,那么直线y=x-$\frac{3}{4}$与y=-x2+2x-1(x>0)相切,
那么y=x与直线y=x-$\frac{3}{4}$的距离是$\frac{3\sqrt{2}}{8}$,利用对称性可知,则|MN|的最小值为$\frac{3\sqrt{2}}{4}$.
则④正确.
故答案为:①③④.
点评 本题考查新定义的理解和运用,考查直线和圆的方程的求法,以及椭圆和抛物线的方程和性质,是一道高考常见的题型.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
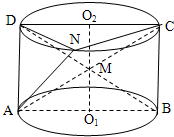 如图,已知矩形ABCD是圆柱O1O2的轴截面,N在上底面的圆周O2上,AC,BD相交于点M.
如图,已知矩形ABCD是圆柱O1O2的轴截面,N在上底面的圆周O2上,AC,BD相交于点M.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{{C}_{4}^{3}C}_{48}^{2}}{{C}_{52}^{5}}$ | B. | $\frac{{{C}_{48}^{3}C}_{4}^{2}}{{C}_{52}^{5}}$ | ||
| C. | 1-$\frac{{{C}_{48}^{1}C}_{4}^{4}}{{C}_{52}^{5}}$ | D. | $\frac{{{C}_{4}^{3}C}_{48}^{2}{{+C}_{4}^{4}C}_{48}^{1}}{{C}_{52}^{5}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com