
【题目】从分别写有![]() 的
的![]() 张卡片中随机抽取
张卡片中随机抽取![]() 张,放回后再随机抽取
张,放回后再随机抽取![]() 张,则抽得的第一张卡片,上的数不大于第二张卡片上的数的概率为( )
张,则抽得的第一张卡片,上的数不大于第二张卡片上的数的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
分析:基本事件总数n=5×5=25,利用列举法求出抽得的第一张卡片上的数不小于第二张卡片上的数包含的基本事件有15个,由此能求出抽得的第一张卡片上的数不大于第二张卡片上的数的概率.
详解:从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,
基本事件总数n=5×5=25,
抽得的第一张卡片上的数不大于第二张卡片上的数包含的基本事件有15个,分别为:
(1,2),(2,3),(1,3),(3,4),(2,4),(1,4),(4,5),(3,5),
(2,5),(1,5),(5,6),(4,6),(3,6),(2,6),(1,6),
则抽得的第一张卡片上的数不小于第二张卡片上的数的概率为p=![]()
故选:D.


科目:高中数学 来源: 题型:
【题目】如图,某公园摩天轮的半径为![]() ,圆心距地面的高度为
,圆心距地面的高度为![]() ,摩天轮做匀速转动,每
,摩天轮做匀速转动,每![]() 转一圈,摩天轮上的点
转一圈,摩天轮上的点![]() 的起始位置在最低点处.
的起始位置在最低点处.
(1)已知在时刻![]() 时
时![]() 距离地面的高度
距离地面的高度![]() ,(其中
,(其中![]() ),求
),求![]() 时
时![]() 距离地面的高度;
距离地面的高度;
(2)当离地面![]() 以上时,可以看到公园的全貌,求转一圈中有多少时间可以看到公园的全貌?
以上时,可以看到公园的全貌,求转一圈中有多少时间可以看到公园的全貌?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面是菱形的四棱锥P﹣ABCD中, ![]() E、F分别为PD、AB的中点,△PAB为等腰直角三角形,PA⊥平面ABCD,PA=1.
E、F分别为PD、AB的中点,△PAB为等腰直角三角形,PA⊥平面ABCD,PA=1.

(1)求证:直线AE∥平面PFC;
(2)求证:PB⊥FC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为双曲线
为双曲线![]() :
: ![]() 的右焦点,过坐标原点的直线依次与双曲线
的右焦点,过坐标原点的直线依次与双曲线![]() 的左、右支交于点
的左、右支交于点![]() ,若
,若![]() ,
, ![]() ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】![]() ,设双曲线的左焦点为
,设双曲线的左焦点为![]() ,连接
,连接![]() ,由对称性可知,
,由对称性可知, ![]() 为矩形,且
为矩形,且![]() ,故
,故![]() ,故选B.
,故选B.
【 方法点睛】本题主要考查双曲线的定义及离心率,属于难题.离心率的求解在圆锥曲线的考查中是一个重点也是难点,一般求离心率有以下几种情况:①直接求出![]() ,从而求出
,从而求出![]() ;②构造
;②构造![]() 的齐次式,求出
的齐次式,求出![]() ;③采用离心率的定义以及圆锥曲线的定义来求解;④根据圆锥曲线的统一定义求解.
;③采用离心率的定义以及圆锥曲线的定义来求解;④根据圆锥曲线的统一定义求解.
【题型】单选题
【结束】
12
【题目】点![]() 到点
到点![]() ,
, ![]() 及到直线
及到直线![]() 的距离都相等,如果这样的点恰好只有一个,那么实数
的距离都相等,如果这样的点恰好只有一个,那么实数![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形, ![]() ,侧面
,侧面![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.

(1)求证: ![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角和直线
所成的角和直线![]() 与平面
与平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:
(Ⅰ)在平行四边形![]() 中,由条件可得
中,由条件可得![]() ,进而可得
,进而可得![]() 。由侧面
。由侧面![]() 底面
底面![]() ,得
,得![]() 底面
底面![]() ,故得
,故得![]() ,所以可证得
,所以可证得![]() 平面
平面![]() .(Ⅱ)先证明平面
.(Ⅱ)先证明平面![]() 平面
平面![]() ,由面面平行的性质可得
,由面面平行的性质可得![]() 平面
平面![]() .(Ⅲ)建立空间直角坐标系,通过求出平面的法向量,根据线面角的向量公式可得
.(Ⅲ)建立空间直角坐标系,通过求出平面的法向量,根据线面角的向量公式可得![]() 。
。
试题解析:
(Ⅰ)证明:在平行四边形![]() 中,
中,
∵![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∵侧面![]() 底面
底面![]() ,且
,且![]() ,
,
∴![]() 底面
底面![]() ,
,
又![]() 底面
底面![]() ,
,
∴![]() ,
,
又![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅱ)证明:∵![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
同理![]() 平面
平面![]() ,
,
又![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅲ)解:由![]() 底面
底面![]() ,
, ![]() ,可得
,可得![]() ,
, ![]() ,
, ![]() 两两垂直,
两两垂直,
建立如图空间直角坐标系![]() ,
,

则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
, ![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
, ![]() ,
,
易得平面![]() 的法向量
的法向量![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则:
,则:
由![]() ,得
,得![]() ,
,
令![]() ,得
,得![]() ,
,
∵直线![]() 与平面
与平面![]() 所成的角和此直线与平面
所成的角和此直线与平面![]() 所成的角相等,
所成的角相等,
∴![]() ,即
,即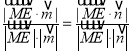 ,
,
∴![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
故![]() .
.
点睛:用向量法确定空间中点的位置的方法
根据题意建立适当的空间直角坐标系,由条件确定有关点的坐标,运用共线向量用参数(参数的范围要事先确定)确定出未知点的坐标,根据向量的运算得到平面的法向量或直线的方向向量,根据所给的线面角(或二面角)的大小进行运算,进而求得参数的值,通过与事先确定的参数的范围进行比较,来判断参数的值是否符合题意,进而得出点是否存在的结论。
【题型】解答题
【结束】
21
【题目】如图,椭圆![]() 上的点到左焦点的距离最大值是
上的点到左焦点的距离最大值是![]() ,已知点
,已知点![]() 在椭圆上,其中
在椭圆上,其中![]() 为椭圆的离心率.
为椭圆的离心率.

(1)求椭圆的方程;
(2)过原点且斜率为![]() 的直线交椭圆于
的直线交椭圆于![]() 、
、![]() 两点,其中
两点,其中![]() 在第一象限,它在
在第一象限,它在![]() 轴上的射影为点
轴上的射影为点![]() ,直线
,直线![]() 交椭圆于另一点
交椭圆于另一点![]() .证明:对任意的
.证明:对任意的![]() ,点
,点![]() 恒在以线段
恒在以线段![]() 为直径的圆内.
为直径的圆内.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}的前n项和为Sn,且![]() =9,S6=60.
=9,S6=60.
(I)求数列{an}的通项公式;
(II)若数列{bn}满足bn+1﹣bn=![]() (n∈N+)且b1=3,求数列
(n∈N+)且b1=3,求数列![]() 的前n项和Tn.
的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com