
【题目】如图:在五面体![]() 中,四边形
中,四边形![]() 是正方形,
是正方形,![]() ,
,![]() ,
,
![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】分析:第一问证明面面垂直,在证明的过程中,利用常规方法,抓住面面垂直的判定定理,找出相应的垂直关系证得结果,第二问求的是线面角的正弦值,利用空间向量,将其转化为直线的方向向量与平面的法向量所成角的余弦值的绝对值,从而求得结果.
详解:(1)证明:因为![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,故平面
,故平面![]() 平面
平面![]() .
.
(2)解:由已知![]() ,所以
,所以![]() 平面
平面![]() .
.
又平面![]() 平面
平面![]() ,故
,故![]() .
.
所以四边形![]() 为等腰梯形.
为等腰梯形.
又![]() ,所以
,所以![]() ,易得
,易得![]() ,令
,令![]() ,
,
如图,以![]() 为原点,以
为原点,以![]() 的方向为
的方向为![]() 轴正方向,建立空间直角坐标系
轴正方向,建立空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,由
,由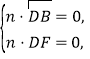
所以 取
取![]() ,则
,则![]() ,
,![]() ,得
,得![]() ,
,
 .
.
设直线与平面![]() 所成的角为
所成的角为![]() ,则
,则![]() .
.
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.



科目:高中数学 来源: 题型:
【题目】基于移动互联技术的共享单车被称为“新四大发明”之一,短时间内就风靡全国,带给人们新的出行体验![]() 某共享单车运营公司的市场研究人员为了解公司的经营状况,对该公司最近六个月内的市场占有率进行了统计,结果如下表:
某共享单车运营公司的市场研究人员为了解公司的经营状况,对该公司最近六个月内的市场占有率进行了统计,结果如下表:
月份 |
|
|
|
|
|
|
月份代码x | 1 | 2 | 3 | 4 | 5 | 6 |
市场占有率 | 11 | 13 | 16 | 15 | 20 | 21 |
![]() 请在给出的坐标纸中作出散点图,并用相关系数说明可用线性回归模型拟合月度市场占有率y与月份代码x之间的关系;
请在给出的坐标纸中作出散点图,并用相关系数说明可用线性回归模型拟合月度市场占有率y与月份代码x之间的关系;
![]() 求y关于x的线性回归方程,并预测该公司2018年2月份的市场占有率;
求y关于x的线性回归方程,并预测该公司2018年2月份的市场占有率;
![]() 根据调研数据,公司决定再采购一批单车扩大市场,现有采购成本分别为1000元
根据调研数据,公司决定再采购一批单车扩大市场,现有采购成本分别为1000元![]() 辆和800元
辆和800元![]() 辆的A,B两款车型报废年限各不相同
辆的A,B两款车型报废年限各不相同![]() 考虑到公司的经济效益,该公司决定先对两款单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表如下:
考虑到公司的经济效益,该公司决定先对两款单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表如下:
报废年限 车型 | 1年 | 2年 | 3年 | 4年 | 总计 |
A | 10 | 30 | 40 | 20 | 100 |
B | 15 | 40 | 35 | 10 | 100 |
经测算,平均每辆单车每年可以为公司带来收入500元![]() 不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且用频率估计每辆单车使用寿命的概率,以每辆单车产生利润的期望值为决策依据
不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且用频率估计每辆单车使用寿命的概率,以每辆单车产生利润的期望值为决策依据![]() 如果你是该公司的负责人,你会选择采购哪款车型?
如果你是该公司的负责人,你会选择采购哪款车型?
参考数据:![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数![]() ,
,
回归直线方程为![]() 其中:
其中:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,G是线段AD延长线一点,![]() ,
,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,F是线段PG的中点;
,F是线段PG的中点;

![]() 求证:
求证:![]() 平面PAC;
平面PAC;
![]() 若
若![]() 时,求平面PCF与平面PAG所成二面角的余弦值.
时,求平面PCF与平面PAG所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】众所周知,大型网络游戏(下面简称网游)的运行必须依托于网络的基础上,否则会出现频繁掉线的情况,进而影响游戏的销售和推广.某网游经销商在甲地区![]() 个位置对两种类型的网络(包括“电信”和“网通”)在相同条件下进行游戏掉线测试,得到数据如下:
个位置对两种类型的网络(包括“电信”和“网通”)在相同条件下进行游戏掉线测试,得到数据如下:
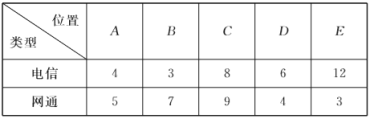
(Ⅰ)如果在测试中掉线次数超过![]() 次,则网络状况为“糟糕”,否则为“良好”,那么在犯错误的概率不超过
次,则网络状况为“糟糕”,否则为“良好”,那么在犯错误的概率不超过![]() 的前提下,能否说明网络状况与网络的类型有关?
的前提下,能否说明网络状况与网络的类型有关?
(Ⅱ)若该游戏经销商要在上述接受测试的电信的![]() 个地区中任选
个地区中任选![]() 个作为游戏推广,求
个作为游戏推广,求![]() 、
、![]() 两地区至少选到一个的概率.
两地区至少选到一个的概率.
参考公式:![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】1642年,帕斯卡发明了一种可以进行十进制加减法的机械计算机![]() 年,莱布尼茨改进了帕斯卡的计算机,但莱布尼兹认为十进制的运算在计算机上实现起来过于复杂,随即提出了“二进制”数的概念
年,莱布尼茨改进了帕斯卡的计算机,但莱布尼兹认为十进制的运算在计算机上实现起来过于复杂,随即提出了“二进制”数的概念![]() 之后,人们对进位制的效率问题进行了深入的研究
之后,人们对进位制的效率问题进行了深入的研究![]() 研究方法如下:对于正整数
研究方法如下:对于正整数![]() ,
,![]() ,我们准备
,我们准备![]() 张不同的卡片,其中写有数字0,1,…,
张不同的卡片,其中写有数字0,1,…,![]() 的卡片各有
的卡片各有![]() 张
张![]() 如果用这些卡片表示
如果用这些卡片表示![]() 位
位![]() 进制数,通过不同的卡片组合,这些卡片可以表示
进制数,通过不同的卡片组合,这些卡片可以表示![]() 个不同的整数
个不同的整数![]() 例如
例如![]() ,
,![]() 时,我们可以表示出
时,我们可以表示出![]() 共
共![]() 个不同的整数
个不同的整数![]() 假设卡片的总数
假设卡片的总数![]() 为一个定值,那么
为一个定值,那么![]() 进制的效率最高则意味着
进制的效率最高则意味着![]() 张卡片所表示的不同整数的个数
张卡片所表示的不同整数的个数![]() 最大
最大![]() 根据上述研究方法,几进制的效率最高?
根据上述研究方法,几进制的效率最高?![]()
![]()
A. 二进制 B. 三进制 C. 十进制 D. 十六进制
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最大值为
的最大值为![]() ,其图像相邻的两条对称轴之间的距离为
,其图像相邻的两条对称轴之间的距离为![]() ,且
,且![]() 的图像关于点
的图像关于点![]() 对称,则下列结论正确的是( ).
对称,则下列结论正确的是( ).
A.函数![]() 的图像关于直线
的图像关于直线![]() 对称
对称
B.当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]()
C.若![]() ,则
,则![]() 的值为
的值为![]()
D.要得到函数![]() 的图像,只需要将
的图像,只需要将![]() 的图像向右平移
的图像向右平移![]() 个单位
个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com