
����Ŀ�����������������98��Ԫ����һ̨���ػ�����������Ͷ������ʹ�ã��ƻ���һ��ά�ޡ���������12��Ԫ���ӵڶ��꿪ʼ��ÿ������ά�ޡ��������ñ���һ������4��Ԫ���û���ʹ�ú�ÿ���������Ϊ50��Ԫ����ʹ��x������ػ�����ӯ����Ϊy��Ԫ��
(��)д��y��x֮��ĺ�����ϵʽ��
(��)�ӵڼ��꿪ʼ���û�����ʼӯ����ӯ����Ϊ��ֵ����
(��)ʹ��������Ի����Ĵ������������֣�
(1)����ƽ��ӯ����ﵽ���ֵʱ����30��Ԫ�۸����û�����
(2)��ӯ����ﵽ���ֵʱ����12��Ԫ�۸����û�����
�����о�һ�����ַ���������Ϊ��������˵�����ɣ�
���𰸡�����) ![]() ���������ӵ�3�꿪ʼӯ�����������������ȽϺ���.
���������ӵ�3�꿪ʼӯ�����������������ȽϺ���.
��������
���������������ʹ��x����������Ϊ![]() ��ÿ��֧����ά�ޱ������ù���һ�Ȳ����У��ɵȲ��������ʽ�ɵ�ʹ��x������֧�����������ȥ��֧����ɵ�ʹ��x������ػ�����ӯ�������Ӷ���y��x֮��ĺ�����ϵʽ.
��ÿ��֧����ά�ޱ������ù���һ�Ȳ����У��ɵȲ��������ʽ�ɵ�ʹ��x������֧�����������ȥ��֧����ɵ�ʹ��x������ػ�����ӯ�������Ӷ���y��x֮��ĺ�����ϵʽ.
�������ⲻ��ʽ![]() ��ɵ�
��ɵ�![]() �ķ�Χ���Ӷ�֪�����ӵ����꿪ʼӯ��.
�ķ�Χ���Ӷ�֪�����ӵ����꿪ʼӯ��.
����)��(1)��ƽ��ӯ����Ϊ��![]()
��![]() ������Ҫ����ʽ��������ֵ���Ӷ���ȷ��ʲôʱ����ƽ��ӯ����ﵽ���ֵ��������������õ���������
������Ҫ����ʽ��������ֵ���Ӷ���ȷ��ʲôʱ����ƽ��ӯ����ﵽ���ֵ��������������õ���������
(2)ӯ����y=��2x2��40x��98��һ�����κ�������ͨ���䷽��������ֵ���Ӷ���ȷ��ʲôʱ��ӯ����ﵽ���ֵ��������������õ���������
�����߽��бȽϣ���֪�ĸ�������������
��������������������![]() ��x
��x![]() N*��. 3��
N*��. 3��
�������ⲻ��ʽ![]() ��
��![]() .
.
![]() .����x
.����x![]() N*,��3��x��17���ʴӵ�3�꿪ʼӯ��. 7��
N*,��3��x��17���ʴӵ�3�꿪ʼӯ��. 7��
������(1)��ƽ��ӯ����Ϊ��![]()
![]() �����ҽ���
�����ҽ���![]() ʱ����x=7ʱ�Ⱥų�����
ʱ����x=7ʱ�Ⱥų�����
������2008�꣬��ƽ��ӯ����ﵽ���ֵ������������12��7+30��114��Ԫ��
(2)ӯ����y=��2x2��40x��98=��(x��10)2��102����x=10ʱ��ymax=102.
�ʵ�2011�꣬ӯ����ﵽ���ֵ����������102+12��114��Ԫ .
ӯ����ﵽ�����ֵ��ͬ�������������õ�ʱ��϶̣��ʷ������ȽϺ����� 12��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
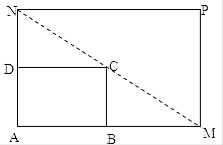
����Ŀ����ͼ��ʾ����һ���λ�̳ABCD������һ������ľ��λ�̳AMPN��Ҫ��B��AM�ϣ�D��AN�ϣ��ҶԽ���MN��C�㣬��֪|AB|=3����|AD|=2��
��1����AN�ij�Ϊx�ף���x��ʾ����AMPN�������
��2��Ҫʹ����AMPN���������32ƽ��������AN�ij�Ӧ��ʲô��Χ�ڣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������f��x��=log3��2��x���Ķ������ǣ� ��
A.[2��+����B.��2��+����C.��������2��D.��������2]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC���ڽ�A��B��C�ĶԱ߷ֱ�Ϊa��b��c.��֪a��bcos C��csin B.
��1����B����2����b��2�����ABC��������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() ��
��![]() ��
��![]() ����
Ϊ����![]() ��ǰ
��ǰ![]() ��ͣ���
��ͣ���![]() ��
��![]() ��
��![]() .
.
��1��������![]() ��
��![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2����![]() ��������
��������![]() ��ǰ
��ǰ![]() ���
���![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ij����Ʒÿ�յ�������y����λ�����������ۼ۸�x����λ����Ԫ/�֣�1��x��5�����㣺��1��x��3ʱ��y=a��x��4��2 +![]() ��aΪ����������3��x��5ʱ��y=kx+7��k��0������֪�����ۼ۸�Ϊ3��Ԫ/��ʱ��ÿ�տ��۳�����Ʒ4�֣������ۼ۸�x����3��5]�仯ʱ�����������Ϊ2�֣�
��aΪ����������3��x��5ʱ��y=kx+7��k��0������֪�����ۼ۸�Ϊ3��Ԫ/��ʱ��ÿ�տ��۳�����Ʒ4�֣������ۼ۸�x����3��5]�仯ʱ�����������Ϊ2�֣�
��1����a��k��ֵ����ȷ��y����x�ĺ�������ʽ��
��2��������Ʒ�����۳ɱ�Ϊ1��Ԫ/�֣���ȷ�����ۼ۸�x��ֵ��ʹ��ÿ�����۸���Ʒ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC��������ԭ�㣬������x���ϣ������ʵ���![]() ������һ������ǡ����������
������һ������ǡ����������![]() �Ľ��㣬
�Ľ��㣬
����������ԲC�ı����̣�
����������ԲC���ҽ���![]() ��ֱ��l����ԲC��A��B���㣬��y����M�㣬��
��ֱ��l����ԲC��A��B���㣬��y����M�㣬��![]()
![]() Ϊ��ֵ��
Ϊ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ�ٰ��˶���ʱ����һ��1������28��ͬѧ�μӱ�������15�˲μ���Ӿ��������8�˲μ��ᄊ��������14�˲μ����������ͬʱ�μ���Ӿ���ᄊ��������3�ˣ�ͬʱ�μ���Ӿ�������������3�ˣ�û����ͬʱ�μ������������ͬʱ�μ��ᄊ����������������ǣ� ����
A.3B.4C.5D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾���������25��Ԫ����һ���µ��豸��Ͷ���豸��ÿ������Ϊ21��Ԫ.�ù�˾��![]() ����Ҫ�����豸��ά���˹��ʵȷ���
����Ҫ�����豸��ά���˹��ʵȷ���![]() ����Ϣ����ͼ .
����Ϣ����ͼ .

��1����![]() ��
��
��2�����������豸�ڼ����ù�˾��ʼ������
��3�������豸ʹ�ö����꣬�ù�˾����ƽ���������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com