
����Ŀ��ij����Ϊ�˽�Ͻ��ס��������������ÿ���ƽ���������ʱ��������Ͻ��ס���������������������ȡ��100λ���˽��е��飬�����ÿ��ÿ���ƽ���������ʱ��������λ��Сʱ�����ʱ�䰴��[0��0.5����[0.5��1��������[4��4.5]���ٵ���ֳ�9�飬�Ƴ�������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��

������ͼ��a��ֵ��
�����Ƹ�����ס��������������ÿ���ƽ���������ʱ��������λ����
��III����[1.5��2����[2��2.5���������в��÷ֲ������ȡ9�ˣ��ٴ���9���������ȡ2�ˣ����ȡ������ǡ�ö���ͬһ����ĸ��ʣ�
���𰸡���1��a=0.40��2��2.06��3��![]()
��������
��I����Ƶ�ʺ�Ϊ1�з������a��ֵ��
��II��������λ������Ƶ����������λ���Ĵ�С��
��III�����÷ֲ������������ȡ�������������û����¼���������ĸ���ֵ��
��I���⣺��Ƶ�ʷֲ�ֱ��ͼ����֪��Ͻ��ס��������������ÿ���ƽ���������ʱ������[0��0.5����Ƶ��Ϊ0.08��0.5=0.04��
ͬ������[0.5��1����[1,1.5����[1.5��2��[2��2.5����[2.5��3��[3��3.5����[3.5��4����[4��4.5]��Ƶ�ʷֱ�Ϊ0.08��0.15��0.5a��0.25��0.15��0.07��0.04��0.02
��![]()
���a=0.40��
��II���⣺�����ʱ��������λ��ΪmСʱ��
��Ϊǰ5���Ƶ��֮��Ϊ0.04+0.08+0.15+0.20+0.25=0.72��0.5��
��ǰ4���Ƶ��֮��Ϊ0.04+0.08+0.15+0.20=0.47��0.5������2��m��2.5��
��0.50����m![]() 2��=0.5
2��=0.5![]() 0.47�����m=2.06��
0.47�����m=2.06��
���Թ��Ƹ�����ס��������������ÿ���ƽ���������ʱ��������λ��Ϊ2.06Сʱ��
��III���⣺�������ƽ������ʱ����[1.5��2����[2��2.5���е������ֱ���20�ˡ�25�ˣ����ֲ�����ķ����ֱ��ȡ4�ˡ�5�ˣ�����A��B��C��D��a��b��c��d��e��9���������ȡ2�ˣ�����36�֣��ֱ�Ϊ��
��A��B������A��C������A��D������A��a������A��b������A��c������A��d������A��e������B��C������B��D������B��a������B��b������B��c������B��d������B��e������C��D������C��a������C��b������C��c������C��d������C��e������D��a������D��b������D��c������D��d������D��e������a��b������a��c������a��d������a��e������b��c������b��d������b��e������c��d������c��e������d��e��
��ͬһ����У���A��B������A��C������A��D������B��C������B��D������C��D������a��b������a��c������a��d������a��e������b��c������b��d������b��e������c��d����c��e������d��e������16�֣��ʳ�ȡ������ǡ�ö���ͬһ����ĸ���![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������̨![]() �У�
��![]() ��
��![]() �ֱ�ΪAC��CB���е㣮
�ֱ�ΪAC��CB���е㣮

��1����֤��ƽ��![]() ��
��
��2����![]() ��
��![]() ����֤��ƽ��
����֤��ƽ��![]()
![]() ƽ��
ƽ��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��M��N��P�ֱ���������ABCD��A1B1C1D1����AB��BC��DD1�ϵĵ�.
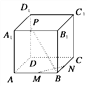
(1)��![]() ����֤�����۵�P��DD1������ƶ�������BP��MN��
����֤�����۵�P��DD1������ƶ�������BP��MN��
(2)��DD1���Ƿ���������ĵ�P��ʹ��ƽ��APC1��ƽ��ACC1��֤����Ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������{an}��n��1��n��N������a1=2��a2=6���ң�an+2��an+1������an+1��an��=2����[x]��ʾ������x�������������[ ![]() +
+ ![]() +��+
+��+ ![]() ]= ��
]= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������![]() �������ⳤ��Ϊ2��
�������ⳤ��Ϊ2�� ![]() Ϊ
Ϊ![]() �е㣬���ÿռ�����֪ʶ���������⣺
�е㣬���ÿռ�����֪ʶ���������⣺
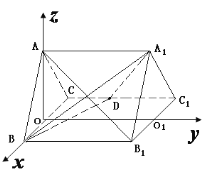
��1����֤![]() ��
��![]() ��
��
��2��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������κ���f��x��=ax3+bx2+cx+d��a��0�����������壺��f�䣨x���Ǻ���y=f��x���ĵ�����f�壨x����f�䣨x���ĵ�����������f�壨x��=0��ʵ����x0 �� ��Ƶ㣨x0 �� f��x0����Ϊ����y=f��x���ġ��յ㡱������̽�����֣��κ�һ�����κ������С��յ㡱���κ�һ�����κ������жԳ����ģ��ҡ��յ㡱���ǶԳ����ģ��躯��g��x��=2x3��3x2+ ![]() ����g��
����g�� ![]() ��+g��
��+g�� ![]() ��+��+g��
��+��+g�� ![]() ��=�� ��
��=�� ��
A.100
B.50
C.![]()
D.0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|x+a|+|x+ ![]() |��a��0��
|��a��0��
��1����a=2ʱ����ʽf��x����3�Ľ⼯��
��2��֤���� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��8����ѧ���μӱ����ĵ÷��þ�Ҷͼ��ʾ����ͼ�����о�Ϊʮλ����ҶΪ��λ�������������ݵ�ƽ�����ͷ���ֱ��ǣ� �� ![]()
A.91 5.5
B.91 5
C.92 5.5
D.92 5
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com