
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其中F1、F2为左右焦点,O为坐标原点,直线l与椭圆交于P(x1、y1),Q(x2,y2)两个不同点,当直线l过椭圆C右焦点F2且倾斜角为$\frac{π}{4}$时,原点O到直线l的距离为$\frac{\sqrt{2}}{2}$,又椭圆上的点到焦点F2的最近距离为$\sqrt{3}$-1
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其中F1、F2为左右焦点,O为坐标原点,直线l与椭圆交于P(x1、y1),Q(x2,y2)两个不同点,当直线l过椭圆C右焦点F2且倾斜角为$\frac{π}{4}$时,原点O到直线l的距离为$\frac{\sqrt{2}}{2}$,又椭圆上的点到焦点F2的最近距离为$\sqrt{3}$-1分析 (1)由题意可设直线l的方程为y=x-c,则有$\frac{c}{\sqrt{2}}=\frac{\sqrt{2}}{2}$,得c=1.再由椭圆上的点到焦点F2的最近距离为a-c=$\sqrt{3}-1$,得a=$\sqrt{3},b=\sqrt{2}$.由此求得椭圆C的方程;
(2)当直线l的斜率不存在时,P,Q两点关于x轴对称,可得x1=x2,y1=-y2,再由平行四边形OQNP面积为$\sqrt{6}$,可得|ON|•|PQ|=$2\sqrt{6}$;
当直线l的斜率存在时,设直线l为y=kx+m,和椭圆方程联立,可得(2+3k2)x2+6kmx+3m2-6=0.由△>0,得3k2+2>m2,再由一元二次方程的根与系数的关系得${x}_{1}+{x}_{2}=-\frac{6km}{2+3{k}^{2}},{x}_{1}{x}_{2}=\frac{3{m}^{2}-6}{2+3{k}^{2}}$,由弦长公式求得|PQ|,由点到直线的距离公式求得O到l的距离为d,代入△POQ的面积可得3k2+2=2m2,满足△>0.
设M是ON与PQ的交点,则$|OM{|}^{2}=(\frac{{x}_{1}+{x}_{2}}{2})^{2}+(\frac{{y}_{1}+{y}_{2}}{2})^{2}=\frac{9{k}^{2}}{4{m}^{2}}+\frac{1}{{m}^{2}}=\frac{1}{2}(3-\frac{1}{{m}^{2}})$,$|PQ{|}^{2}=(1+{k}^{2})\frac{24(3{k}^{2}+2-{m}^{2})}{(2+3{k}^{2})^{2}}=\frac{2(2{m}^{2}+1)}{{m}^{2}}=2(2+\frac{1}{{m}^{2}})$,进一步得到
$|OM{|}^{2}•|PQ{|}^{2}=(3-\frac{1}{{m}^{2}})(2+\frac{1}{{m}^{2}})≤\frac{25}{4}$,当且仅当$3-\frac{1}{{m}^{2}}=2+\frac{1}{{m}^{2}}$,即m=$±\sqrt{2}$时等号成立.由此可得|OM|•|PQ|的最大值为$\frac{5}{2}$,|ON|•|PQ|=2|OM|•|PQ|的最大值为5.
解答 解:(1)∵直线l的倾斜角为$\frac{π}{4}$,设F2(C,0),则直线l的方程为y=x-c,
则$\frac{c}{\sqrt{2}}=\frac{\sqrt{2}}{2}$,得c=1.
由椭圆的几何性质可得椭圆上的点到焦点F2的最近距离为a-c=$\sqrt{3}-1$,得a=$\sqrt{3},b=\sqrt{2}$.
∴椭圆C的方程为$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$;
(2)当直线l的斜率不存在时,P,Q两点关于x轴对称,则x1=x2,y1=-y2,
由P(x1,y1)在椭圆上,则$\frac{{{x}_{1}}^{2}}{3}+\frac{{{y}_{1}}^{2}}{2}=1$,而$S=2|{x}_{1}{y}_{1}|=\sqrt{6}$,则$|{x}_{1}|=\frac{\sqrt{6}}{2},|{y}_{1}|=1$.
知|ON|•|PQ|=$2\sqrt{6}$;
当直线l的斜率存在时,设直线l为y=kx+m,代入$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$可得,
2x2+3(kx+m)2=6,即(2+3k2)x2+6kmx+3m2-6=0.
△>0,即3k2+2>m2,${x}_{1}+{x}_{2}=-\frac{6km}{2+3{k}^{2}},{x}_{1}{x}_{2}=\frac{3{m}^{2}-6}{2+3{k}^{2}}$,
|PQ|=$\sqrt{1+{k}^{2}}|{x}_{1}-{x}_{2}|=\sqrt{1+{k}^{2}}\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}\frac{2\sqrt{6}\sqrt{3{k}^{2}+2-{m}^{2}}}{2+3{k}^{2}}$.
设O到l的距离为d,
则d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$,${S}_{△POQ}=\frac{1}{2}d|PQ|=\frac{1}{2}|m|\frac{2\sqrt{6}\sqrt{3{k}^{2}+2-{m}^{2}}}{2+3{k}^{2}}=\frac{\sqrt{6}}{2}$.
化为9k4+12k2+4-12m2k2-8m2+4m4=0.
得到(3k2+2-2m2)2=0,则3k2+2=2m2,满足△>0.
由前知,$\frac{{x}_{1}+{x}_{2}}{2}=-\frac{3k}{2m},\frac{{y}_{1}+{y}_{2}}{2}=k(\frac{{x}_{1}+{x}_{2}}{2})+m=-\frac{3{k}^{2}}{2m}+m=\frac{1}{m}$,
设M是ON与PQ的交点,则
$|OM{|}^{2}=(\frac{{x}_{1}+{x}_{2}}{2})^{2}+(\frac{{y}_{1}+{y}_{2}}{2})^{2}=\frac{9{k}^{2}}{4{m}^{2}}+\frac{1}{{m}^{2}}=\frac{1}{2}(3-\frac{1}{{m}^{2}})$,
$|PQ{|}^{2}=(1+{k}^{2})\frac{24(3{k}^{2}+2-{m}^{2})}{(2+3{k}^{2})^{2}}=\frac{2(2{m}^{2}+1)}{{m}^{2}}=2(2+\frac{1}{{m}^{2}})$,
$|OM{|}^{2}•|PQ{|}^{2}=(3-\frac{1}{{m}^{2}})(2+\frac{1}{{m}^{2}})≤\frac{25}{4}$,当且仅当$3-\frac{1}{{m}^{2}}=2+\frac{1}{{m}^{2}}$,即m=$±\sqrt{2}$时等号成立.
综上可知,|OM|•|PQ|的最大值为$\frac{5}{2}$,|ON|•|PQ|=2|OM|•|PQ|的最大值为5.
点评 本题主要考查圆锥曲线的定义的应用,在解决涉及到圆锥曲线上的点与焦点之间的关系的问题中,圆锥曲线的定义往往是解题的突破口,考查直线与圆锥曲线的位置关系,涉及直线与圆锥曲线的关系问题,常联立直线与圆锥曲线方程,利用一元二次方程的根与系数的关系求解,该题运算量大,要求学生具有较强的运算能力,属难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
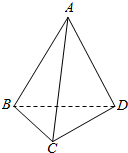 如图,在四面体ABCD中,已知∠ABD=∠CBD=60°,AB=BC=2,
如图,在四面体ABCD中,已知∠ABD=∠CBD=60°,AB=BC=2,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
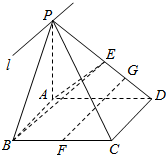 如图,四棱锥P-ABCD,底面ABCD为平行四边形,E、F分别为 PD、BC的中点,面PAB∩面PCD=l.
如图,四棱锥P-ABCD,底面ABCD为平行四边形,E、F分别为 PD、BC的中点,面PAB∩面PCD=l.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图AB是圆O的直径,AF⊥AB,弦CD交AB、AF分别于E、F,交圆于点C.
如图AB是圆O的直径,AF⊥AB,弦CD交AB、AF分别于E、F,交圆于点C.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,已知AB为半圆O的直径,AB=4,C为平面上一点,过点C作半圆的切线CD,过A点作AD⊥CD于D,角半圆于点E,DE=1,则BC的长为( )
如图,已知AB为半圆O的直径,AB=4,C为平面上一点,过点C作半圆的切线CD,过A点作AD⊥CD于D,角半圆于点E,DE=1,则BC的长为( )| A. | 1 | B. | 2 | C. | 1.5 | D. | 2.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
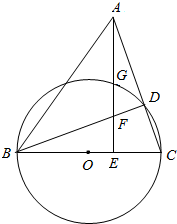 如图,以△ABC的边BC为直径作圆O交AC于D,过A点作AE⊥BC于E,AE交圆O于点G,交BD于点F.
如图,以△ABC的边BC为直径作圆O交AC于D,过A点作AE⊥BC于E,AE交圆O于点G,交BD于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com