
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调递减区间;
的单调递减区间;
(2)当![]() 时,设函数
时,设函数![]() .若存在区间
.若存在区间![]() ,使得函数
,使得函数![]() 在
在![]() 上的值域为
上的值域为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)当![]() 时,减区间为
时,减区间为![]() ,
,![]() ;当
;当![]() 时,减区间为
时,减区间为![]() ;当
;当![]() 时,减区间为
时,减区间为![]() ,
,![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析:(Ⅰ)对f(x)进行求导,讨论a=1,a>1.0<a<1,利用导数为负,求函数的减区间;(Ⅱ)要求存在区间,使f(x)在[m,n]上的值域是[k(m+2)-2,k(n+2)-2],将其转化为g(x)=k(x+2)-2在![]() 上至少有两个不同的正根,再利用导数求出k的取值范围
上至少有两个不同的正根,再利用导数求出k的取值范围
试题解析:(Ⅰ) ![]() 的定义域为
的定义域为![]() ,
, ![]()
①当![]() 时,
时, ![]() .
.
由![]() 得
得![]() 或
或![]() .∴当
.∴当![]() ,
, ![]() 时,
时, ![]() 单调递减.
单调递减.
∴![]() 的单调递减区间为
的单调递减区间为![]() ,
,![]() .
.
②当![]() 时,恒有
时,恒有![]() ,∴
,∴![]() 单调递减.
单调递减.
∴![]() 的单调递减区间为
的单调递减区间为![]() .
.
③当![]() 时,
时, ![]() .
.
由![]() 得
得![]() 或
或![]() .∴当
.∴当![]() ,
, ![]() 时,
时, ![]() 单调递减.
单调递减.
∴![]() 的单调递减区间为
的单调递减区间为![]() ,
,![]() .
.
综上,当![]() 时,
时, ![]() 的单调递减区间为
的单调递减区间为![]() ,
,![]() ;
;
当![]() 时,
时, ![]() 的单调递减区间为
的单调递减区间为![]() ;
;
当![]() 时,
时, ![]() 的单调递减区间为
的单调递减区间为![]() ,
,![]() .
.
(Ⅱ)当![]() 时,
时, ![]() ,
, ![]() ,
, ![]()
当![]() 时,
时, ![]() ,∴
,∴![]() 在
在![]() 上单调递增.
上单调递增.
又![]() 在
在![]() 上恒成立.
上恒成立.
![]() 在
在![]() 上单调递增.
上单调递增.
由题意,得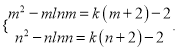
原问题转化为关于![]() 的方程
的方程![]() 在
在![]() 上有两个不相等的实数根.
上有两个不相等的实数根.
即方程![]() 在
在![]() 上有两个不相等的实数根.
上有两个不相等的实数根.
令函数![]() .
.
则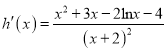 . 令函数
. 令函数![]() .
.
则![]() 在
在![]() 上有
上有![]() .
.
故![]() 在
在![]() 上单调递增.
上单调递增.
![]() ,
,
![]() 当
当![]() 时,有
时,有![]() 即
即![]() .∴
.∴![]() 单调递减;
单调递减;
当![]() 时,有
时,有![]() 即
即![]() ,∴
,∴![]() 单调递增.
单调递增.
![]() ,
, ![]() ,
,
![]() 的取值范围为
的取值范围为![]()


科目:高中数学 来源: 题型:
【题目】经销商经销某种农产品,在一个销售季度内,每售出![]() 该产品获利润500元,未售出的产品,每
该产品获利润500元,未售出的产品,每![]() 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了
亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了![]() 该农产品.以
该农产品.以![]() (
(![]() )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量, ![]() (单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:元)表示下一个销售季度内经销该农产品的利润.
(Ⅰ)将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)根据直方图估计利润![]() 不少于57000元的概率.
不少于57000元的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将7名应届师范大学毕业生分配到3所中学任教.
(1)4个人分到甲学校,2个人分到乙学校,1个人分到丙学校,有多少种不同的分配方案?
(2)一所学校去4个人,另一所学校去2个人,剩下的一个学校去1个人,有多少种不同的分配方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为调查高三年级学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图1)和女生身高情况的频率分布直方图(图2).已知图1中身高在170~175cm的男生人数有16人.

(1)根据频率分布直方图,完成下列的![]() 列联表,并判断能有多大(百分几)的把握认为“身高与性别有关”?
列联表,并判断能有多大(百分几)的把握认为“身高与性别有关”?
|
| 总计 | |
男生身高 | |||
女神身高 | |||
总计 |
(2)在上述80名学生中,从身高在170-175cm之间的学生按男、女性别分层抽样的方法,抽出5人,从这5人中选派3人当旗手,求3人中恰好有一名女生的概率.
参考公式: 
参考数据:
| 0.025 | 0.610 | 0.005 | 0.001 |
| 5.024 | 4.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数),在以
为参数),在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 是圆心在极轴上,且经过极点的圆.已知曲线
是圆心在极轴上,且经过极点的圆.已知曲线![]() 上的点
上的点 对应的参数
对应的参数![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若点![]() ,
, ![]() 在曲线
在曲线![]() 上,求
上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,(
,( ![]() 为常数)
为常数)
(1)若![]() 在
在![]() 处的切线方程为
处的切线方程为![]() (
(![]() 为常数),求
为常数),求![]() 的值;
的值;
(2)设函数![]() 的导函数为
的导函数为![]() ,若存在唯一的实数
,若存在唯一的实数![]() ,使得
,使得![]() 与
与![]() 同时成立,求实数
同时成立,求实数![]() 的取值范围;
的取值范围;
(3)令![]() ,若函数
,若函数![]() 存在极值,且所有极值之和大于
存在极值,且所有极值之和大于![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com