练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    直线y=x+b能作为下列函数图象的切线的是    （写出所有符合题意的函数的序号）
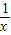    ①f（x）=    ②f（x）=sinx    ③f（x）=x（x2+1）④f（x）=gx．
    【答案】分析：先求出函数的导函数，然后根据直线y=x+b能作为下列函数图象的切线，根据导数与切线斜率的关系建立等式，看是否成立即可．
    解答：解：①f′（x）=-=不成立；
        ②f′（x）=cosx=可以成立；
        ③f′（x）=3x2+1=不成立；
        ④f′（x）=ex=可成立．
    故直线y=x+b能作为②④函数图象的切线，
    故答案为：②④．
    点评：本题主要考查了利用导数研究曲线上某点切线方程，关键利用导数与切线斜率的关系，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    直线y=
    1
    2
    x+b能作为下列函数图象的切线的是
     
    （写出所有符合题意的函数的序号）
    ①f（x）=
    1
    x
        ②f（x）=sinx    ③f（x）=x（x2+1）④f（x）=gx．

    查看答案和解析>>

    科目：高中数学 来源：设计选修数学－2-2苏教版 苏教版 题型：044

    对于函数f(x)＝和f(x)＝，判断直线y＝2x＋b是否能作为上述函数图象的切线？若能，求出切点坐标，若不能，简述理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    直线y=数学公式x+b能作为下列函数图象的切线的是________（写出所有符合题意的函数的序号）
    ①f（x）=数学公式 　②f（x）=sinx　　③f（x）=x（x2+1）④f（x）=gx．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    直线y=
    1
    2
    x+b能作为下列函数图象的切线的是______（写出所有符合题意的函数的序号）
    ①f（x）=
    1
    x
        ②f（x）=sinx    ③f（x）=x（x2+1）④f（x）=gx．

    查看答案和解析>>

    同步练习册答案