
【题目】拿破仑为人好学,是法兰西科学院院士,他对数学方面很感兴趣,在行军打仗的空闲时间,经常研究平面几何。他提出了著名的拿破仑定理:以三角形各边为边分别向外(内)侧作等边三角形,则它们的中心构成一个等边三角形。如图所示,以等边![]() 的三条边为边,向外作
的三条边为边,向外作![]() 个正三角形,取它们的中心
个正三角形,取它们的中心![]() ,顺次连接,得到
,顺次连接,得到![]() ,图中阴影部分为
,图中阴影部分为![]() 与
与![]() 的公共部分。若往
的公共部分。若往![]() 中投掷一点,则该点落在阴影部分内的概率为( )
中投掷一点,则该点落在阴影部分内的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
【题目】现行的个税法修正案规定:个税免征额由原来的2000元提高到3500元,并给出了新的个人所得税税率表:
全月应纳税所得额 | 税率 |
不超过1500元的部分 | 3% |
超过1500元至4500元的部分 | 10% |
超过4500元至9000元的部分 | 20% |
超过9000元至35000元的部分 | 25% |
…… | … |
例如某人的月工资收入为5000元,那么他应纳个人所得税为:![]() (元).
(元).
(Ⅰ)若甲的月工资收入为6000元,求甲应纳的个人收的税;
(Ⅱ)设乙的月工资收入为![]() 元,应纳个人所得税为
元,应纳个人所得税为![]() 元,求
元,求![]() 关于
关于![]() 的函数;
的函数;
(Ⅲ)若丙某月应纳的个人所得税为1000元,给出丙的月工资收入.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是圆
是圆![]() 上的任意一点,
上的任意一点,![]() 是过点
是过点![]() 且与
且与![]() 轴垂直的直线,
轴垂直的直线,![]() 是直线
是直线![]() 与
与![]() 轴的交点,点
轴的交点,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() .当点
.当点![]() 在圆
在圆![]() 上运动时,记点
上运动时,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,证明:直线
,证明:直线![]() 过定点
过定点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2,AD=1,M为AB的中点,将△ADM沿DM翻折.在翻折过程中,当二面角A—BC—D的平面角最大时,其正切值为( )
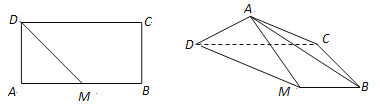
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是一个
是一个![]() 的方格表,在每一个小方格内各填一个正整数.若
的方格表,在每一个小方格内各填一个正整数.若![]() 中的一个
中的一个![]() 方格表的所有数的和为10的倍数,则称其为“好矩形”;若
方格表的所有数的和为10的倍数,则称其为“好矩形”;若![]() 中的一个
中的一个![]() 的小方格不包含于任何一个好矩形,则称其为“坏格”.求
的小方格不包含于任何一个好矩形,则称其为“坏格”.求![]() 中坏格个数的最大值.
中坏格个数的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水果的价格会受到需求量和天气的影响.某采购员定期向某批发商购进某种水果,每箱水果的价格会在当日市场价的基础上进行优惠,购买量越大优惠幅度越大,采购员通过对以往的10组数据进行研究,发现可采用![]() 来作为价格的优惠部分
来作为价格的优惠部分![]() (单位:元/箱)与购买量
(单位:元/箱)与购买量![]() (单位:箱)之间的回归方程,整理相关数据得到下表(表中
(单位:箱)之间的回归方程,整理相关数据得到下表(表中![]() ):
):
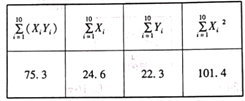
(1)根据参考数据,
①建立![]() 关于
关于![]() 的回归方程;
的回归方程;
②若当日该种水果的市场价为200元/箱,估算购买100箱该种水果所需的金额(精确到0.1元).
(2)在样本中任取一点,若它在回归曲线上或上方,则称该点为高效点.已知这10个样本点中,高效点有4个,现从这10个点中任取3个点,设取到高效点的个数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为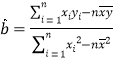 ,
,![]() ,参考数据:
,参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是平面内凸三十五边形的35个顶点,且
是平面内凸三十五边形的35个顶点,且![]() 中任何两点之间的距离不小于
中任何两点之间的距离不小于![]() . 证明:从这35个点中可以选出五个点,使得这五个点中任意两点之间的距离不小于3.
. 证明:从这35个点中可以选出五个点,使得这五个点中任意两点之间的距离不小于3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一布袋中装有![]() 个小球,甲,乙两个同学轮流且不放回的抓球,每次最少抓一个球,最多抓三个球,规定:由乙先抓,且谁抓到最后一个球谁赢,那么以下推断中正确的是( )
个小球,甲,乙两个同学轮流且不放回的抓球,每次最少抓一个球,最多抓三个球,规定:由乙先抓,且谁抓到最后一个球谁赢,那么以下推断中正确的是( )
A. 若![]() ,则乙有必赢的策略B. 若
,则乙有必赢的策略B. 若![]() ,则甲有必赢的策略
,则甲有必赢的策略
C. 若![]() ,则甲有必赢的策略D. 若
,则甲有必赢的策略D. 若![]() ,则乙有必赢的策略
,则乙有必赢的策略
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com