
【题目】已知直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
(1)若直线![]() 斜率为1,过椭圆
斜率为1,过椭圆![]() 的右焦点,求弦
的右焦点,求弦![]() 的长;
的长;
(2)若![]() ,且
,且![]() 为锐角,求直线
为锐角,求直线![]() 斜率的取值范围.
斜率的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)联立直线方程和椭圆方程,利用弦长公式求得弦AB的长;
(2)直线l方程为y=kx+2,A(x1,y1),B(x2,y2),与椭圆联立,注意到交于不同的两点A、B,△>0且∠AOB为锐角,转化为![]() 利用韦达定理,代入化简,求直线l的斜率k的取值范围.
利用韦达定理,代入化简,求直线l的斜率k的取值范围.
(1)由题意知,右焦点F2(![]() ,0),则直线l的方程为y=x﹣
,0),则直线l的方程为y=x﹣![]() ,
,
联立 ,得5x2﹣
,得5x2﹣![]() x+8=0.
x+8=0.
设A(x1,y1),B(x2,y2),
则![]() ,
,
∴|AB|![]() ;
;
(2)若![]() ,则l的方程为y=kx+2,设A(x1,y1),B(x2,y2).
,则l的方程为y=kx+2,设A(x1,y1),B(x2,y2).
联立
∴![]() ,
,![]()
由△=(16k)2﹣4(1+4k2)12>0,16k2﹣3(1+4k2)>0,4k2﹣3>0,得![]() .①
.①
又∠AOB为锐角![]() ,
,
∴![]()
又y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4
∴x1x2+y1y2=(1+k2)x1x2+2k(x1+x2)+4
![]()
![]()
![]()
∴![]() .②
.②
综①②可知![]() ,
,
∴k的取值范围是 .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为椭圆
为椭圆![]() 的左焦点,直线
的左焦点,直线![]() ,
,![]() 为椭圆上任意一点,证明:点
为椭圆上任意一点,证明:点![]() 到
到![]() 的距离是点
的距离是点![]() 到
到![]() 距离的
距离的![]() 倍.
倍.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为菱形且∠DAB=60°,O为AD中点.
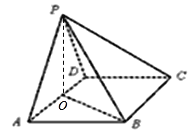
(Ⅰ)若PA=PD,求证:平面POB⊥平面PAD;
(Ⅱ)若平面PAD⊥平面ABCD,且PA=PD=AD=2,试问在线段PC上是否存在点M,使二面角M-BO-C的大小为30°,如存在,求![]() 的值,如不存在,说明理由.
的值,如不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在![]() 上的函数
上的函数![]() 满足:对任意的
满足:对任意的![]() ,当
,当![]() 时,都有
时,都有![]() .
.
(1)若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 为周期函数,证明:
为周期函数,证明:![]() 是常值函数;
是常值函数;
(3)若![]() 在
在![]() 上满足:
上满足:![]() ,
,![]() ,
,![]() ,
,
①记![]() (
(![]() ),求数列
),求数列![]() 的通项公式;② 求
的通项公式;② 求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙二人去看望高中数学张老师,期间他们做了一个游戏,张老师的生日是![]() 月
月![]() 日,张老师把
日,张老师把![]() 告诉了甲,把
告诉了甲,把![]() 告诉了乙,然后张老师列出来如下10个日期供选择: 2月5日,2月7日,2月9日,3月2日,3月7日,5月5日,5月8日,7月2日,7月6日,7月9日.看完日期后,甲说“我不知道,但你一定也不知道”,乙听了甲的话后,说“本来我不知道,但现在我知道了”,甲接着说,“哦,现在我也知道了”.请问张老师的生日是_______.
告诉了乙,然后张老师列出来如下10个日期供选择: 2月5日,2月7日,2月9日,3月2日,3月7日,5月5日,5月8日,7月2日,7月6日,7月9日.看完日期后,甲说“我不知道,但你一定也不知道”,乙听了甲的话后,说“本来我不知道,但现在我知道了”,甲接着说,“哦,现在我也知道了”.请问张老师的生日是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρ=2cos θ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是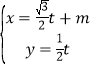 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)当m=2时,直线l与曲线C交于A、B两点,求|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com