
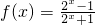 (x∈R).
(x∈R). ,
, <2,-2<-
<2,-2<- <0,
<0, <1,即-1<f(x)<1,
<1,即-1<f(x)<1,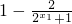 )-(1-
)-(1-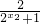 )=
)=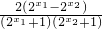 ,
,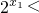
 ,
, =
= =
=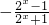 =-f(x),
=-f(x),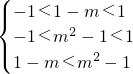 ,解得1<m
,解得1<m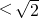 .
.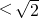 }.
}. ,利用指数函数的值域及不等式的性质即可求得函数值域;
,利用指数函数的值域及不等式的性质即可求得函数值域;

科目:高中数学 来源: 题型:解答题
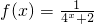 (x∈R).
(x∈R).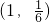 在f(x)的图象上,判断其关于点
在f(x)的图象上,判断其关于点 对称的点是否仍在f(x)的图象上;
对称的点是否仍在f(x)的图象上; 对称;
对称;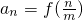 (m∈{N}^{*},n=1,2,…,m),求数列{an}的前m项和Sm.
(m∈{N}^{*},n=1,2,…,m),求数列{an}的前m项和Sm.查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省台州外国语学校高一(下)第一次月考数学试卷(解析版) 题型:解答题
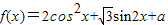 (x∈R).
(x∈R).查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省黄冈市武穴市梅川高中高三(上)11月月考数学试卷(理科)(解析版) 题型:解答题
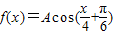 ,x∈R,且
,x∈R,且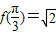
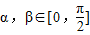 ,
, ,
,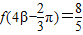 ,求cos(α+β)的值.
,求cos(α+β)的值.查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省肇庆市f封开县南丰中学高三数学复习试卷D(必修4)(解析版) 题型:解答题
 (x∈R).
(x∈R).查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省高三第三次月考文科数学卷 题型:解答题
(满分12分)已知函数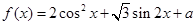 (x∈R).
(x∈R).
(1)若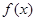 有最大值2,求实数a的值;
有最大值2,求实数a的值;
(2)求函数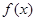 的单调递增区间.
的单调递增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com