
【题目】已知函数![]()
(1)若![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,若函数
时,若函数![]() 有两个极值点
有两个极值点![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)f(x)=alnx﹣x+1,利用导数性质结合分类讨论思想,能求出实数a的取值范围.
(2)g(x)=alnx﹣x+![]() ,g′(x)=
,g′(x)=![]() ,由此利用导数性质能求出当x=e时,t(x)取得最大值,最大值为t(e)=
,由此利用导数性质能求出当x=e时,t(x)取得最大值,最大值为t(e)=![]() .
.
(1)![]() ,
,![]()
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 内单调递减,
内单调递减,
则有![]() ,从而
,从而![]()
当![]() 时,
时,![]() ,得
,得![]() ,当
,当![]() ,有
,有![]() ,则
,则![]() 在
在![]() 上内单调递增,此时
上内单调递增,此时![]() ,与
,与![]() 恒成立矛盾,因此不符合题意
恒成立矛盾,因此不符合题意
综上实数![]() 的取值范围为
的取值范围为![]() .
.
( 2 )![]() 则
则![]()
由已知,可得![]() ,即方程
,即方程![]() 有2个不相等的实数根
有2个不相等的实数根![]() ,
,
则 ,解得
,解得 ,其中
,其中![]()
而g(x2)﹣g(x1)=alnx2﹣x2+![]() ﹣alnx1+x1﹣
﹣alnx1+x1﹣![]() =aln
=aln![]() +(x1﹣x2)+(
+(x1﹣x2)+(![]() ﹣
﹣![]() )
)
=(x2+![]() )lnx22+
)lnx22+![]() ﹣x2+
﹣x2+![]() +x2
+x2
=2[(![]() +x2)lnx2+
+x2)lnx2+![]() ﹣x2],
﹣x2],
由![]() 可得
可得![]() ,又
,又![]() ,所以
,所以![]()
设![]() ,
,![]()
![]() ,由
,由![]() ,则
,则![]() ,故
,故![]()
所以![]() 在
在![]() 单调递增,当
单调递增,当![]() 时,
时,![]() 取得最大值,最大值为
取得最大值,最大值为![]()


科目:高中数学 来源: 题型:
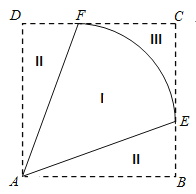
【题目】某地拟规划种植一批芍药,为了美观,将种植区域(区域I)设计成半径为1km的扇形![]() ,中心角
,中心角![]() (
(![]() ).为方便观赏,增加收入,在种植区域外围规划观赏区(区域II)和休闲区(区域III),并将外围区域按如图所示的方案扩建成正方形
).为方便观赏,增加收入,在种植区域外围规划观赏区(区域II)和休闲区(区域III),并将外围区域按如图所示的方案扩建成正方形![]() ,其中点
,其中点![]() ,
,![]() 分别在边
分别在边![]() 和
和![]() 上.已知种植区、观赏区和休闲区每平方千米的年收入分别是10万元、20万元、20万元.
上.已知种植区、观赏区和休闲区每平方千米的年收入分别是10万元、20万元、20万元.
(1)要使观赏区的年收入不低于5万元,求![]() 的最大值;
的最大值;
(2)试问:当![]() 为多少时,年总收入最大?
为多少时,年总收入最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解本市居民的生活成本,甲乙丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得的数据分别绘制成频率分布直方图(如图所示),记甲乙丙所调查数据的标准差分别为![]() ,
,![]() ,
,![]() ,则它们的大小关系为__________.
,则它们的大小关系为__________.

(甲)

(乙)

(丙)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() .
.
(1)若直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,当
,当![]() 时,求实数
时,求实数![]() 的值;
的值;
(2)若![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作圆
作圆![]() 的两条切线
的两条切线![]() 、
、![]() ,切点为
,切点为![]() 、
、![]() ,试探究:直
,试探究:直![]() 是否过定点.若存在,请求出定点的坐标;否则,说明理由.
是否过定点.若存在,请求出定点的坐标;否则,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列四个说法中:
①![]() 与
与![]() 表示同一函数;
表示同一函数;
②已知函数![]() 的定义域为
的定义域为![]() ,则
,则![]() 的定义域为
的定义域为![]() ;
;
③不等式![]() 对于
对于![]() 恒成立,则
恒成立,则![]() 的取值范围是
的取值范围是![]() ;
;
④对于集合![]() ,
,![]() ,
,
若![]() ,则
,则![]() 的取值范围
的取值范围![]() ,其中正确说法的序号是______.
,其中正确说法的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知整数对排列如下:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4)......则第60个整数对是( )
A.(5,7)B.(11,5)C.(7,5)D.(5,11)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com