
在直角坐标系 中,已知点
中,已知点 ,点
,点 在
在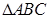 三边围成的区域(含边界)上,且
三边围成的区域(含边界)上,且 .
.
(1)若 ,求
,求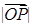 ;
;
(2)用 表示
表示 ,并求
,并求 的最大值.
的最大值.
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
一农民有基本农田2亩,根据往年经验,若种水稻,则每季亩产量为400公斤;若种花生,则每季亩产量为100公斤.但水稻成本较高,每季每亩240元,而花生只需80元;且花生每公斤卖5元,稻米每公斤卖3元.现该农民手头有400元,两种作物各种多少,才能获得最大收益?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为保增长、促发展,某地计划投资甲、乙两项目,市场调研得知,甲项目每投资百万元需要配套电能2万千瓦,可提供就业岗位24个,增加GDP260万元;乙项目每项投资百万元需要配套电能4万千瓦,可提供就业岗位32个,增加GDP200万元,已知该地为甲、乙两项目最多可投资3 000万元,配套电能100万千瓦,并要求它们提供的就业岗位不少于800个,如何安排甲、乙两项目的投资额,增加的GDP最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某营养师要为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物、6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物、6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物、42个单位的蛋白质和54个单位的维生素C.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com