
分析 设三角形面积为S,由正弦定理可得b+2c=6absinC=12S,解得S=$\frac{\sqrt{8+4bc}}{12}$,由b2+4c2=8≥4bc,解得:bc≤2,当且仅当b=2c时等号成立,可得S≤$\frac{1}{3}$,当且仅当b=2c时等号成立,解得b,c,利用三角形面积公式可求sinA的值,求得cosA,利用余弦定理即可求解.
解答 解:设三角形面积为S,∵sinB+2sinC=6bsinAsinC,且由正弦定理可得:$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R$,
∴b+2c=6absinC=12S,解得:S=$\frac{b+2c}{12}$=$\frac{\sqrt{(b+2c)^{2}}}{12}$=$\frac{\sqrt{{b}^{2}+4{c}^{2}+4bc}}{12}$=$\frac{\sqrt{8+4bc}}{12}$,
∵b2+4c2=8≥4bc,解得:bc≤2,当且仅当b=2c时等号成立,
∴S≤$\frac{1}{3}$,当且仅当b=2c时等号成立,
∴当b=2c时,b2+4c2=8,解得:b=2,c=1,S=$\frac{1}{3}$=$\frac{1}{2}$bcsinA=$\frac{1}{2}×2×1×$sinA,解得:sinA=$\frac{1}{3}$,
∴由三角形为锐角三角形,解得:cosA=$\sqrt{1-si{n}^{2}A}$=$\frac{2\sqrt{2}}{3}$,
∴此时,a2=b2+c2-2bccosA=4+1-2×2×1×$\frac{2\sqrt{2}}{3}$=$\frac{15-8\sqrt{2}}{3}$.
故答案为:$\frac{15-8\sqrt{2}}{3}$.
点评 本题主要考查了三角形面积公式,正弦定理,余弦定理,基本不等式的应用,熟练掌握和灵活应用相关公式定理是解题的关键,属于基本知识的考查.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
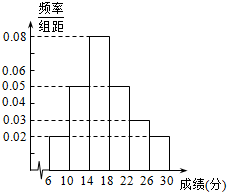 为了解某省去年高三考生英语听力成绩,现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如下方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30],如图是按上述分组方法得到的频率分布直方图.
为了解某省去年高三考生英语听力成绩,现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如下方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30],如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某楼盘开展套餐促销优惠活动,优惠方案如下:选择套餐一的客户可获得优惠2万元,选择套餐二的客户可获得优惠5万元,选择套餐三的客户可获得优惠3万元.根据以往的统计结果绘出参与活动的统计图如图所示,现将频率视为概率.
某楼盘开展套餐促销优惠活动,优惠方案如下:选择套餐一的客户可获得优惠2万元,选择套餐二的客户可获得优惠5万元,选择套餐三的客户可获得优惠3万元.根据以往的统计结果绘出参与活动的统计图如图所示,现将频率视为概率.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com