【题目】（5分）《九章算术》“竹九节”问题：现有一根9节的竹子，自上而下各节的容积成等差数列，上面4节的容积共3升，下面3节的容积共4升，则第五节的容积为（ ）
A. 1升 B. 
升 C. 
升 D. 
升
科目：高中数学 来源： 题型：
【题目】某单位员工
人参加“学雷锋”志愿活动，按年龄分组：第
组
，第
组
,第
组
,第
组
,第
组
，得到的频率分布直方图如图所示.
（1）下表是年龄的频率分布表，求正整数
的值；
区间 |
|
|
|
|
|
人数 |
|
|
|
|
|
（2）现在要从年龄较小的第
组中用分层抽样的方法抽取
人，年龄在第组抽取的员工的人数分别是多少？
（3）在（2）的前提下，从这人中随机抽取人参加社区宣传交流活动，求至少有人年龄在第组的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知曲线
，
，则下面结论正确的是（ ）
A. 把
上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移
个单位长度，得到曲线
B. 把上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线
C. 把上各点的横坐标缩短到原来的
倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线
D. 把上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，
.
（1）若
在区间
上不是单调函数，求实数
的范围；
（2）若对任意
，都有
恒成立，求实数
的取值范围；
（3）当
时，设
，对任意给定的正实数，曲线
上是否存在两点
，
，使得
是以
（为坐标原点）为直角顶点的直角三角形，而且此三角形斜边中点在
轴上？请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知双曲线C:x2-y2=1及直线l:y=kx+1.
(1)若l与C有两个不同的交点,求实数k的取值范围;
(2)若l与C交于A,B两点,且线段AB中点的横坐标为
,求线段AB的长.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四边形ABCD是边长为1的正方形，MD⊥ABCD，NB⊥ABCD．且MD＝NB＝1．则下列结论中：
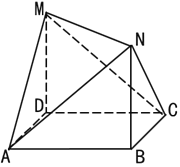
①MC⊥AN
②DB∥平面AMN
③平面CMN⊥平面AMN
④平面DCM∥平面ABN
所有假命题的个数是（ ）
A.0B.1C.2D.3
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，平面四边形
中，
，
是
，
中点，
，
，
，将
沿对角线折起至
，使平面
平面
，则四面体
中，下列结论不正确的是（ ）
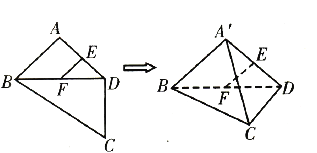
A. 
平面
B. 异面直线
与
所成的角为
C. 异面直线
与
所成的角为
D. 直线与平面所成的角为
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某高校在2019年的自主招生笔试成绩（满分200分）中，随机抽取100名考生的成绩，按此成绩分成五组，得到如下的频率分布表：
组号 | 分组 | 频数 | 频率 |
第一组 |
| 15 |
|
第二组 |
| 25 | 0.25 |
第三组 |
| 30 | 0.3 |
第四组 |
|
|
|
第五组 |
| 10 | 0.1 |
（1）求频率分布表中
，
，
的值；
（2）估计笔试成绩的平均数及中位数（同一组中的数据用该组区间的中点值作代表）；（精确到0.1）
（3）若从第四组、第五组的学生中按组用分层抽样的方法抽取6名学生参加面试，用简单随机抽样方法从6人中抽取2人作为正、副小组长，求“抽取的2人为同一组”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
