
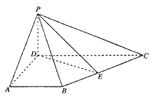
【题目】如图,四边形![]() 为梯形,
为梯形, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若有,请找出具体位置,并进行证明:若无,请分析说明理由.
?若有,请找出具体位置,并进行证明:若无,请分析说明理由.
科目:高中数学 来源: 题型:
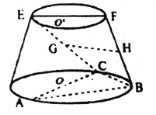
【题目】在如图所示的圆台中,![]() 是下底面圆
是下底面圆![]() 的直径,
的直径,![]() 是上底面圆
是上底面圆![]() 的直径,
的直径,![]() 是圆台的一条母线.
是圆台的一条母线.
(Ⅰ)已知![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)已知![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值
的余弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2008年至2014年中,每年的居民人均纯收入y(单位:千元)的数据如下表:
年 份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.7 | 3.6 | 3.3 | 4.6 | 5.4 | 5.7 | 6.2 |
对变量t与y进行相关性检验,得知t与y之间具有线性相关关系.
(1)求y关于t的线性回归方程;
(2)预测该地区2017年的居民人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
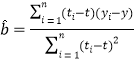 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天气预报是气象专家根据预测的气象资料和专家们的实际经验,经过分析推断得到的,在现实的生产生活中有着重要的意义,某快餐企业的营销部门对数据分析发现,企业经营情况与降雨填上和降雨量的大小有关.
(1)天气预报所,在今后的三天中,每一天降雨的概率为40%,该营销部分通过设计模拟实验的方法研究三天中恰有两天降雨的概率,利用计算机产生0大9之间取整数值的随机数,并用![]() 表示下雨,其余
表示下雨,其余![]() 个数字表示不下雨,产生了20组随机数:
个数字表示不下雨,产生了20组随机数:
![]()
求由随机模拟的方法得到的概率值;
(2)经过数据分析,一天内降雨量的大小![]() (单位:毫米)与其出售的快餐份数
(单位:毫米)与其出售的快餐份数![]() 成线性相关关系,该营销部门统计了降雨量与出售的快餐份数的数据如下:
成线性相关关系,该营销部门统计了降雨量与出售的快餐份数的数据如下:
![]()
试建立![]() 关于
关于![]() 的回归方程,为尽量满足顾客要求又不在造成过多浪费,预测降雨量为6毫米时需要准备的快餐份数.(结果四舍五入保留整数)
的回归方程,为尽量满足顾客要求又不在造成过多浪费,预测降雨量为6毫米时需要准备的快餐份数.(结果四舍五入保留整数)
附注:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
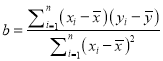 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆的一组![]() 等分点分别涂上红色或蓝色,从任意一点开始,按逆时针方向依次记录
等分点分别涂上红色或蓝色,从任意一点开始,按逆时针方向依次记录![]() 个点的颜色,称为该圆的一个“
个点的颜色,称为该圆的一个“![]() 阶段序”,当且仅当两个
阶段序”,当且仅当两个![]() 阶色序对应位置上的颜色至少有一个不相同时,称为不同的
阶色序对应位置上的颜色至少有一个不相同时,称为不同的![]() 阶色序.若某圆的任意两个“
阶色序.若某圆的任意两个“![]() 阶段序”均不相同,则称该圆为“
阶段序”均不相同,则称该圆为“![]() 阶魅力圆”.“3阶魅力圆”中最多可有的等分点个数为( )
阶魅力圆”.“3阶魅力圆”中最多可有的等分点个数为( )
A.4 B.6
C. 8 D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读:
已知![]() 、
、![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
解法如下:![]() ,
,
当且仅当![]() ,即
,即![]() 时取到等号,
时取到等号,
则![]() 的最小值为
的最小值为![]() .
.
应用上述解法,求解下列问题:
(1)已知![]() ,
,![]() ,求
,求![]() 的最小值;
的最小值;
(2)已知![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(3)已知正数![]() 、
、![]() 、
、![]() ,
,![]() ,
,
求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com