
【题目】已知f(x)=|xex|,又g(x)=[f(x)]2﹣tf(x)(t∈R),若方程g(x)=﹣2有4个不同的根,则t的取值范围为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:解:f(x)= ![]() , 当x≥0时,f′(x)=ex+xex=(1+x)ex>0,
, 当x≥0时,f′(x)=ex+xex=(1+x)ex>0,
∴f(x)在[0,+∞)上是增函数,
当x<0时,f′(x)=﹣ex﹣xex=(﹣1﹣x)ex ,
∴当x<﹣1时,f′(x)>0,当﹣1<x<0时,f′(x)<0,
∴f(x)在(﹣∞,﹣1]上是增函数,在(﹣1,0)上是减函数.
当x=﹣1时,f(x)取得极大值f(﹣1)= ![]() .
.
令f(x)=λ,
又f(x)≥0,f(0)=0,
则当λ<0时,方程f(x)=λ无解;
当λ=0或λ> ![]() 时,方程f(x)=λ有一解;
时,方程f(x)=λ有一解;
当λ= ![]() 时,方程f(x)=λ有两解;
时,方程f(x)=λ有两解;
当0<λ< ![]() 时,方程f(x)=λ有三解.
时,方程f(x)=λ有三解.
∵方程g(x)=﹣2有4个不同的根,即[f(x)]2﹣tf(x)+2=0有4个不同的解,
∴关于λ的方程λ2﹣tλ+2=0在(0, ![]() )和(
)和( ![]() ,+∞)上各有一解.
,+∞)上各有一解.
∴ 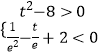 ,解得t>
,解得t> ![]() .
.
故选C.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】某校高三2班有48名学生进行了一场投篮测试,其中男生28人,女生20人.为了了解其投篮成绩,甲、乙两人分别对全班的学生进行编号(1~48号),并以不同的方法进行数据抽样,其中一人用的是系统抽样,另一人用的是分层抽样.若此次投篮考试的成绩大于或等于80分视为优秀,小于80分视为不优秀,以下是甲、乙两人分别抽取的样本数据:
(Ⅰ)从甲抽取的样本数据中任取两名同学的投篮成绩,记“抽到投篮成绩优秀”的人数为X,求X的分布列和数学期望;
(Ⅱ)请你根据乙抽取的样本数据完成下列2×2列联表,判断是否有95%以上的把握认为投篮成绩和性别有关?
(Ⅲ)判断甲、乙各用何种抽样方法,并根据(Ⅱ)的结论判断哪种抽样方法更优?说明理由.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2-ax+a2-13=0},B={x|x2-4x+3=0},C={x|x2—3x=0}.
(1)若A∩B=A![]() B,求a的值;
B,求a的值;
(2)若![]() ,
,![]() 求a的值.
求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的一个对称中心为
的一个对称中心为![]() ,其图像上相邻两个最高点间的距离为
,其图像上相邻两个最高点间的距离为![]() .
.

(1)求函数![]() 的解析式;
的解析式;
(2)用“五点作图法”在给定的坐标系中作出函数![]() 在一个周期内的图像,并写出函数
在一个周期内的图像,并写出函数![]() 的单调递减区间.
的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三国时代吴国数学家赵爽所著《周髀算经》中用赵爽弦图给出了勾股定理的绝妙证明,如图是赵爽弦图,图中包含四个全等的勾股形及一个小正方形,分别涂成朱色和黄色,若朱色的勾股形中较大的锐角α为 ![]() ,现向该赵爽弦图中随机地投掷一枚飞镖,则飞镖落在黄色的小正方形内的概率为 .
,现向该赵爽弦图中随机地投掷一枚飞镖,则飞镖落在黄色的小正方形内的概率为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知AB⊥平面ACD,DE∥AB,△ACD是等腰三角形,∠CAD=120°,AD=DE=2AB. 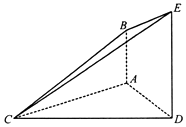
(I)求证:平面BCE⊥平面CDE;
(II)求平面BCE与平面ADEB所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,圆C的参数方程为![]() (α为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系.
(α为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系.
(1)写出圆C的极坐标方程及圆心C的极坐标;
(2)直线l的极坐标方程为![]() 与圆C交于M,N两点,求△CMN的面积.
与圆C交于M,N两点,求△CMN的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体![]() 的棱长为
的棱长为![]() ,
, ![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,过直线
的中点,过直线![]() 的平面分别与棱
的平面分别与棱![]() .
.![]() 交于
交于![]() ,设
,设![]() ,
,![]() ,给出以下四个命题:
,给出以下四个命题:

①平面![]()
![]() 平面
平面![]() ;②当且仅当
;②当且仅当![]() 时,四边形
时,四边形![]() 的面积最小; ③四边形
的面积最小; ③四边形![]() 周长
周长![]() ,
,![]() 是单调函数;④四棱锥
是单调函数;④四棱锥![]() 的体积
的体积![]() 为常函数;
为常函数;
以上命题中真命题的序号为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com