解:(1)由f(m•n)=[f(m)]
n得:f(0)=f(0×0)=[f(0)]
0∵函数f(x)的图象均在x轴的上方,
∴f(0)>0,∴f(0)=1(3分)
∵f(2)=f(1×2)=[f(1)]
2=4,又f(x)>0
∴f(1)=2,f(-1)=f(1)=2(3分)
(2)
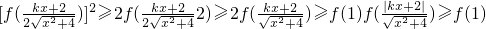
又当x≥0时,其导函数f'(x)>0恒成立,
∴y=f(x)在区间[0,+∞)上为单调递增函数
∴
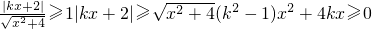
①当k=0时,x∈{0};
②当-1<k<0时,
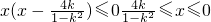
,
∴
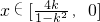
;
③当0<k<1时,
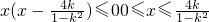
,
∴
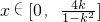
综上所述:当k=0时,x∈{0};当-1<k<0时,
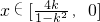
;
当0<k<1时,
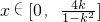
.
分析:(1)由f(m•n)=[f(m)]
n,恒成立,令m=n=0,结合我们易得函数y=f(x)的图象均在x轴的上方,故f(0)>0易得f(0)的值,令m=1,n=2,结合f(2)=4,易得f(1)的值,结合函数y=f(x)是定义域为R的偶函数,可得到f(-1)的值;
(2)由y=f(x)在区间[0,+∞)上为单调递增函数,又由函数为偶函数,故函数在(-∞,0]为单调递减函数,故
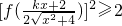
可转化为(k
2-1)x
2+4kx≥0对k值进行分类讨论后,易得结论.
点评:本题考查的知识点是奇偶性与单调性的综合,利用导数研究函数的单调性,利用“凑”的方法处理抽象函数问题求值是解答本题的关键.

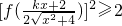 ,其中k∈(-1,1).
,其中k∈(-1,1).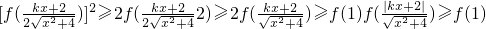
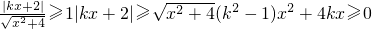
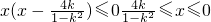 ,
,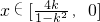 ;
;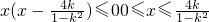 ,
,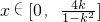
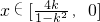 ;
;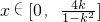 .
.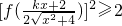 可转化为(k2-1)x2+4kx≥0对k值进行分类讨论后,易得结论.
可转化为(k2-1)x2+4kx≥0对k值进行分类讨论后,易得结论.

 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为