
【题目】已知f(x)=(logmx)2+2logmx﹣3(m>0,且m≠1).
(Ⅰ)当m=2时,解不等式f(x)<0;
(Ⅱ)f(x)<0在[2,4]恒成立,求实数m的取值范围.
【答案】解:(Ⅰ)当m=2时,f(x)<0,
可得(log2x)2+2log2x﹣3<0,
即为﹣3<log2x<1,
解得 ![]() <x<2,
<x<2,
故原不等式的解集为{x| ![]() <x<2};
<x<2};
(Ⅱ)由f(x)<0在[2,4]恒成立,
得﹣3<logmx<1在[2,4]恒成立,
①当m>1时,解得m﹣3<x<m,
即有m﹣3<2且4<m,
解得m>4;
②当0<m<1时,解得m<x<m﹣3,
即有m﹣3>4且m<2,
解得0<m< ![]() .
.
故实数m的取值范围是(0, ![]() )∪(4,+∞).
)∪(4,+∞).
【解析】(1)当m=2时,f(x)<0,可得(log2x)2+2log2x﹣3<0,解得﹣3<log2x<1,再解对数不等式即可得到x的解集,(2)由f(x)<0在[2,4]恒成立,得﹣3<logmx<1在[2,4]恒成立,对m进行分类讨论,从而得到实数m的取值范围.


科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,满足(2b﹣c)cosA=acosC.
(1)求角A;
(2)若 ![]() ,b+c=5,求△ABC的面积.
,b+c=5,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )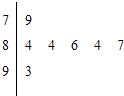
A.84,4.84
B.84,1.6
C.85,1.6
D.85,4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由代数式的乘法法则类比推导向量的数量积的运算法则:
①mn=nm类比得到ab=ba;
②(m+n)t=mt+nt类比得到(a+b)c=ac+bc;
③(mn)t=m(nt) 类比得到(ab)c=a(bc);
④t≠0,mt=rtm=r类比得到p≠0,ap=bpa=b;
⑤|mn|=|m||n|类比得到|ab|=|a||b|;
⑥ ![]() =
= ![]() 类比得到
类比得到 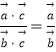 .
.
以上式子中,类比得到的结论正确的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r米,高为h米,体积为V立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12000π元(π为圆周率).
(Ⅰ)将V表示成r的函数V(r),并求该函数的定义域;
(Ⅱ)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形. 
(Ⅰ)求出f(5);
(Ⅱ)利用合情推理的“归纳推理思想”归纳出f(n+1)与f(n)的关系式,并根据你得到的关系式求f(n)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,平面ABCD⊥平面BCE,BE⊥EC.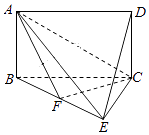
(1)求证:平面AEC⊥平面ABE;
(2)点F在BE上,若DE∥平面ACF,DC=CE= ![]() BC=3,求三棱锥A﹣BCF的体积.
BC=3,求三棱锥A﹣BCF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且Sn+an=1,数列{bn}为等差数列,且b1+b2=b3=3.
(1)求Sn;
(2)求数列(anbn)的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com