[题目]假设小明订了一份报纸.送报人可能在早上6:30﹣7:30之间把报纸送到.小明离家的时间在早上7:00﹣8:00之间.则他在离开家之前能拿到报纸的概率( )A.B.C.D. 题目和参考答案——青夏教育精英家教网—

【题目】假设小明订了一份报纸，送报人可能在早上6：30﹣7：30之间把报纸送到，小明离家的时间在早上7：00﹣8：00之间，则他在离开家之前能拿到报纸的概率（）
A.
B.
C.
D.

【答案】D
【解析】解：设送报人到达的时间为x，小明离家的时间为y，记小明离家前能看到报纸为事件A；以横坐标表示报纸送到时间，以纵坐标表示小明离家时间，建立平面直角坐标系，
小明离家前能得到报纸的事件构成区域如图示：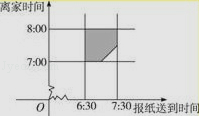

由于随机试验落在方形区域内任何一点是等可能的，所以符合几何概型的条件．
根据题意，只要点落到阴影部分，就表示小明在离开家前能得到报纸，即事件A发生，
所以P（A）= = ，
故选：D．
设送报人到达的时间为x，小明离家的时间为y，则（x，y）可以看成平面中的点，分析可得由试验的全部结果所构成的区域并求出其面积，同理可得事件A所构成的区域及其面积，由几何概型公式，计算可得答案．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】朱载堉(1536～1611)，是中国明代一位杰出的音乐家、数学家和天文历算家，他的著作《律学新说》中制成了最早的“十二平均律”．十二平均律是目前世界上通用的把一组音(八度)分成十二个半音音程的律制，各相邻两律之间的频率之比完全相等，亦称“十二等程律”．即一个八度13个音，相邻两个音之间的频率之比相等，且最后一个音是最初那个音的频率的2倍．设第三个音的频率为，第七个音的频率为，则＝

A. B. C. D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在数列{an}中，a1＝，其前n项和为Sn，且Sn＝an＋1－ (n∈N*)．

(1)求an，Sn；

(2)设bn＝log2(2Sn＋1)－2，数列{cn}满足cn·bn＋3·bn＋4＝1＋(n＋1)(n＋2)·2bn，数列{cn}的前n项和为Tn，求使4Tn>2n＋1－成立的最小正整数n的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在四棱锥P﹣ABCD中，侧面PAD⊥底面ABCD，侧棱PA=PD= ，PA⊥PD，底面ABCD为直角梯形，其中BC∥AD，AB⊥AD，AB=BC=1，O为AD中点．

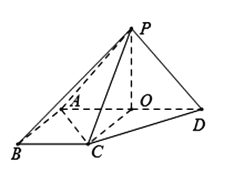
(1) 求直线PB与平面POC所成角的余弦值;

(2)线段上是否存在一点,使得二面角的余弦值为?若存在，求出的值；若不存在，请说明理由.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆的一个焦点为，离心率为. 点为圆上任意一点，为坐标原点.

（Ⅰ）求椭圆的标准方程；

（Ⅱ）记线段与椭圆交点为，求的取值范围；

（Ⅲ）设直线经过点且与椭圆相切，与圆相交于另一点，点关于原点的对称点为，试判断直线与椭圆的位置关系，并证明你的结论.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知数列{an}的前n项和为Sn ，且a2=8，Sn= ﹣n﹣1．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）求数列{ }的前n项和Tn ．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】A、B是治疗同一种疾病的两种药，用若干试验组进行对比试验．每个试验组由4只小白鼠组成，其中2只服用A，另2只服用B，然后观察疗效．若在一个试验组中，服用A有效的小白鼠的只数比服用B有效的多，就称该试验组为甲类组．设每只小白鼠服用A有效的概率为，服用B有效的概率为．
（Ⅰ）求一个试验组为甲类组的概率；
（Ⅱ）观察3个试验组，用ξ表示这3个试验组中甲类组的个数，求ξ的分布列和数学期望．