Question

6．已知抛物线y²=4x的准线与双曲线$\frac{x^2}{a^2}-\frac{y^2}{4}=1$相交于A，B两点，F为抛物线的焦点，∠FAB=45°，则双曲线的离心率为（　　）

• A． 3
• B． 2
• C． $\sqrt{6}$
• D． $\sqrt{3}$

Answer 1

分析 求得抛物线的准线方程，代入双曲线方程，求得A点坐标，由△FAB是等腰直角三角形，根据等腰三角形的性质，$\frac{2\sqrt{1-{a}^{2}}}{a}$=2即可求得a的值，求得c，利用双曲线的离心率公式，即可求得双曲线的离心率．

解答 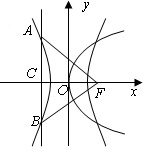解：依题意知抛物线的准线x=-1．代入双曲线方程得
y=±$\frac{2\sqrt{1-{a}^{2}}}{a}$．
不妨设A（-1，$\frac{2\sqrt{1-{a}^{2}}}{a}$），
∵∠FAB=45°，则△FAB是等腰直角三角形，
则丨FC丨=丨AC丨，即$\frac{2\sqrt{1-{a}^{2}}}{a}$=2，解得：a²=$\frac{1}{2}$，
∴c²=a²+b²=$\frac{1}{2}$+4=$\frac{9}{2}$，
∴e=$\frac{c}{a}$=$\sqrt{\frac{{c}^{2}}{{a}^{2}}}$=3，
则双曲线的离心率为3．
故选：A．

点评 本题考查抛物线及双曲线的标准方程及简单几何性质，考查计算能力，属于中档题．