
分析 (Ⅰ)设g(x)=cosx+$\frac{{x}^{2}}{2}$-1,则g'(x)=-sinx+x,x∈[0,+∞),再次构造函数h(x)=-sinx+x,则h'(x)=-cosx+1≥0在x∈[0,+∞)时恒成立,可得g'(x)≥0在[0,+∞)上恒成立,可得cosx+$\frac{{x}^{2}}{2}$-1≥0,即可得证.
(Ⅱ)由(Ⅰ)可知,不等式eax-x-$\frac{{x}^{2}}{2}$-1≥0,对x∈[0,+∞)恒成立,构造函数M(x)=ex-$\frac{1}{2}$x2-x-1,令m(x)=ex-x-1,则m'(x)=ex-1,当x∈[0,+∞)时,m'(x)≥0,可得恒成立,从而得证ex-$\frac{1}{2}$x2-x-1≥0,当a≥1时,不等式f(x)≤eax-2恒成立.
解答 证明:(Ⅰ)不等式sinx-f(x)≥1-$\frac{{x}^{2}}{2}$,
即不等式cosx≥1-$\frac{{x}^{2}}{2}$.…(1分)
设g(x)=cosx+$\frac{{x}^{2}}{2}$-1,则g′(x)=-sinx+x,x∈[0,+∞).
再次构造函数h(x)=-sinx+x,
则h′(x)=-cosx+1≥0在x∈[0,+∞)时恒成立,所以函数h(x)在[0,+∞)上单调递增,所以h(x)≥h(0)=0,
所以g′(x)≥0在[0,+∞)上恒成立,所以函数g(x)在[0,+∞)上单调递增,
所以g(x)≥g(0)=0,
所以cosx+$\frac{{x}^{2}}{2}$-1≥0,即sinx-f(x)≥1-$\frac{{x}^{2}}{2}$成立.
(Ⅱ)由(Ⅰ)的解析可知,当x∈[0,+∞)时,sinx≤x且cosx≥1-$\frac{{x}^{2}}{2}$,
所以f(x)=sinx-cosx=x-(1-$\frac{{x}^{2}}{2}$),
当x-(1-$\frac{{x}^{2}}{2}$)≤eax-2,对x∈[0,+∞)恒成立时,不等式f(x)≤eax-2恒成立,
不等式x-(1-$\frac{{x}^{2}}{2}$)≤eax-2,即eax-x-$\frac{{x}^{2}}{2}$-1≥0,对x∈[0,+∞)恒成立,
构造函数M(x)=ex-$\frac{1}{2}$x2-x-1,
则M'(x)=ex-x-1,
令m(x)=ex-x-1,
则m'(x)=ex-1,当x∈[0,+∞)时,m'(x)≥0,
故m(x)在[0,+∞)上单调递增,
所以m(x)≥m(0)=0,故M'(x)≥0,即M(x)在[0,+∞)上单调递增,
所以M(x)≥M(0)=0,
故ex-$\frac{1}{2}$x2-x-1≥0恒成立,…(11分)
故当a≥1时,eax-x-$\frac{{x}^{2}}{2}$-1≥ex-$\frac{1}{2}$x2-x-1≥0,
即当a≥1时,不等式f(x)≤eax-2恒成立.
点评 本题考查了三角函数恒等变换的应用,考查了导数的概念及应用,考查了转化思想和函数思想的应用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①④ | C. | ②③ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
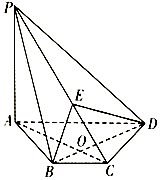 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD交于点O,E为线段PC上的点,且AC⊥BE.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD交于点O,E为线段PC上的点,且AC⊥BE.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 把自然数按如图所示排列起来,从上往下依次为第一行、第二行、第三行…,中间用虚线围起来的一列数,从上往下依次为1、5、13、25、…,按这样的顺序,排在第30个的数是1741.
把自然数按如图所示排列起来,从上往下依次为第一行、第二行、第三行…,中间用虚线围起来的一列数,从上往下依次为1、5、13、25、…,按这样的顺序,排在第30个的数是1741.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
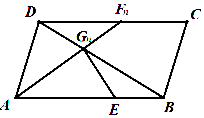 如图,已知点E为平行四边形ABCD的边AB上一点,$\overrightarrow{AE}$=2$\overrightarrow{EB}$,Fn(n∈N*)为边DC上的一列点,连接AFn交BD于Gn,点Gn(n∈N*)满足$\overrightarrow{{G_n}D}$=$\frac{1}{3}$an+1$\overrightarrow{{G_n}A}$-(3an+2)$\overrightarrow{{G_n}E}$,其中数列{an}是首项为1的正项数列,则a4的值为( )
如图,已知点E为平行四边形ABCD的边AB上一点,$\overrightarrow{AE}$=2$\overrightarrow{EB}$,Fn(n∈N*)为边DC上的一列点,连接AFn交BD于Gn,点Gn(n∈N*)满足$\overrightarrow{{G_n}D}$=$\frac{1}{3}$an+1$\overrightarrow{{G_n}A}$-(3an+2)$\overrightarrow{{G_n}E}$,其中数列{an}是首项为1的正项数列,则a4的值为( )| A. | 45 | B. | 51 | C. | 53 | D. | 61 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
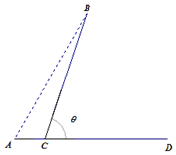 某城市A计划每天从蔬菜基地B处给本市供应蔬菜,为此,准备从主干道AD的C处(不在端点A、D处)做一条道路CB,主干道AD的长为60千米,设计路线如图所示,测得蔬菜基地B在城市A的东偏北60°处,AB长为60千米,设∠BCD=θ,运输汽车在主干道AD上的平均车速为60千米/小时,在道路CB上的平均车速为20千米/小时.
某城市A计划每天从蔬菜基地B处给本市供应蔬菜,为此,准备从主干道AD的C处(不在端点A、D处)做一条道路CB,主干道AD的长为60千米,设计路线如图所示,测得蔬菜基地B在城市A的东偏北60°处,AB长为60千米,设∠BCD=θ,运输汽车在主干道AD上的平均车速为60千米/小时,在道路CB上的平均车速为20千米/小时.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com