
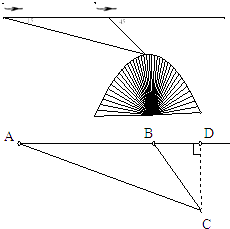
【题目】航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10000m,速度为180km(千米)/h(小时),飞机先看到山顶的俯角为15°,经过420s(秒)后又看到山顶的俯角为45°,求山顶的海拔高度(取 ![]() ,
, ![]() ).
). 
科目:高中数学 来源: 题型:
【题目】(本小题满分为14分)已知定义域为R的函数![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于三角形满足的条件,下列判断正确的是( )
A.a=7,b=14,A=30°,有两解
B.a=30,b=25,A=150°,有一解
C.a=6,b=9,A=45°,有两解
D.b=9,c=10,B=60°,无解
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2﹣ax+b.
(1)若不等式f(x)<0的解集是{x|2<x<3},求不等式bx2﹣ax+1>0的解集;
(2)当b=3﹣a时,对任意的x∈(﹣1,0]都有f(x)≥0成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2+2ax﹣b2+4
(1)若a是从0,1,2三个数中任取的一个数,b是从﹣2,﹣1,0,1,2五个数中任取的一个数,求函数f(x)有零点的概率;
(2)若a是从区间[﹣3,3]上任取的一个数,b是从区间[0,3]上任取的一个数,求函数g(x)=f(x)+5无零点的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x,g(x)=ax+2(a>0),若x1∈[﹣1,2],x2∈[﹣1,2],使得f(x1)=g(x2),则实数a的取值范围是( )
A.![]()
B.![]()
C.(0,3]
D.[3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂对一批产品的质量进行了抽样检测,右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图.已知样本中产品净重在[70,75)克的个数是8个. 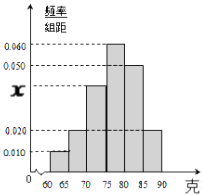
(Ⅰ)求样本容量;
(Ⅱ)若从净重在[60,70)克的产品中任意抽取2个,求抽出的2个产品恰好是净重在[65,70)的产品的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com