
【题目】已知函数![]() 的定义域为
的定义域为![]()
(1)当![]() 时,求函数
时,求函数![]() 的单调递减区间.
的单调递减区间.
(2)若![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)令f![]() (x)<0解得0<x<
(x)<0解得0<x<![]() 或
或![]() 得
得![]() 的单调区间.(2)法一:令g(x)=f(x)-1+sinx+
的单调区间.(2)法一:令g(x)=f(x)-1+sinx+![]() <0在
<0在![]() 上恒成立,利用g(
上恒成立,利用g(![]() )<0,求出a<-1,再对a<-1进行分类讨论.法二:变量分离,当x=0时,不等式恒成立;当
)<0,求出a<-1,再对a<-1进行分类讨论.法二:变量分离,当x=0时,不等式恒成立;当![]()
![]() ,再构造新函数,求最值即可.
,再构造新函数,求最值即可.
(1)![]() 时
时 ![]() ,
,![]()
![]() ,解得
,解得![]() 或
或![]()
所以函数的单调递减区间是![]() ,
,![]()
(2)方法一
![]() ,
,
则只需![]() 在
在![]() 时恒成立,
时恒成立,
则![]() 所以
所以![]()
![]()
因为![]() ,所以
,所以![]()
1)当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,![]() ,符合题意
,符合题意
2)当![]() 时,存在
时,存在![]() ,
,![]() 使得
使得![]() ,
,
①![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,![]() ,符合题意;
,符合题意;
②![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,![]() 时
时![]() 取得最大值;
取得最大值;
因为![]() ,所以
,所以![]() 所以
所以
![]()
令![]() ,其中
,其中![]()
则![]() ,
,
![]() 单调递增,
单调递增,![]() ,所以
,所以![]() ,
,![]() 时
时![]() ,符合题意;
,符合题意;
③![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;![]() ,符合题意。
,符合题意。
所以![]() 的取值范围是
的取值范围是![]()
方法二:
![]() 即
即![]()
当![]() 时,不等式恒成立
时,不等式恒成立
当![]() 时,只需
时,只需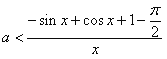 成立
成立
令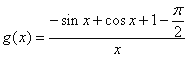 ,则
,则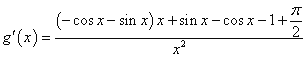
令![]()
则![]()
所以当![]() 时
时![]() ,
,![]() 单调递减
单调递减
当![]() 时
时![]() ,
,![]() 单调递增
单调递增
又因为![]() ,
,![]()
结合单调性可知![]() 时
时![]() ,
,![]() 时
时![]()
即![]() 时
时![]() 单调递减,
单调递减,![]()
![]() 单调递增。
单调递增。
![]() 时,
时,![]() 取得最小值
取得最小值![]()
所以![]() 的取值范围是
的取值范围是![]()


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别是
的左、右焦点分别是![]() 、
、![]() ,离心率
,离心率![]() ,过点
,过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 、
、![]() 两点,
两点, ![]() 的周长为16.
的周长为16.
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 为原点,圆
为原点,圆![]() :
: ![]() (
(![]() )与椭圆
)与椭圆![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 上一动点,若直线
上一动点,若直线![]() 、
、![]() 与
与![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,求证:
两点,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)求![]() 在点P(1,
在点P(1,![]() )处的切线方程;
)处的切线方程;
(2)若关于x的不等式![]() 有且仅有三个整数解,求实数t的取值范围;
有且仅有三个整数解,求实数t的取值范围;
(3)若![]() 存在两个正实数
存在两个正实数![]() ,
,![]() 满足
满足![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 两个城镇相距20公里,设
两个城镇相距20公里,设![]() 是
是![]() 中点,在
中点,在![]() 的中垂线上有一高铁站
的中垂线上有一高铁站![]() ,
,![]() 的距离为10公里.为方便居民出行,在线段
的距离为10公里.为方便居民出行,在线段![]() 上任取一点
上任取一点![]() (点
(点![]() 与
与![]() ,
,![]() 不重合)建设交通枢纽,从高铁站铺设快速路到
不重合)建设交通枢纽,从高铁站铺设快速路到![]() 处,再铺设快速路分别到
处,再铺设快速路分别到![]() ,
,![]() 两处.因地质条件等各种因素,其中快速路
两处.因地质条件等各种因素,其中快速路![]() 造价为3百万元/公里,快速路
造价为3百万元/公里,快速路![]() 造价为2百万元/公里,快速路
造价为2百万元/公里,快速路![]() 造价为4百万元/公里, 设
造价为4百万元/公里, 设![]() ,总造价为
,总造价为![]() (单位:百万元).
(单位:百万元).
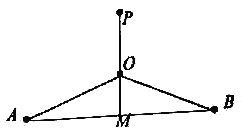
(1)求![]() 关于
关于![]() 的函数关系式,并指出函数的定义域;
的函数关系式,并指出函数的定义域;
(2)求总造价![]() 的最小值,并求出此时
的最小值,并求出此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式![]() .
.
(1)是否存在实数m,使不等式对任意![]() 恒成立?并说明理由.
恒成立?并说明理由.
(2)若不等式对任意![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
(3)若对于![]() ,不等式恒成立,求实数x的取值范围.
,不等式恒成立,求实数x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示:
名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示:

(1)求频率分布直方图中实数![]() 的值;
的值;
(2)估计20名学生成绩的平均数;
(3)从成绩在![]() 的学生中任选2人,求此2人的成绩不都在
的学生中任选2人,求此2人的成绩不都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 两焦点分别为
两焦点分别为![]() 是椭圆在第一象限弧上一点,并满足
是椭圆在第一象限弧上一点,并满足![]() ,过P作倾斜角互补的两条直线
,过P作倾斜角互补的两条直线![]() 分别交椭圆于
分别交椭圆于![]() 两点.
两点.
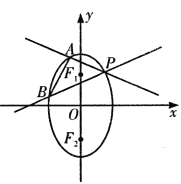
(1)求![]() 点坐标;
点坐标;
(2)求证:直线![]() 的斜率为定值;
的斜率为定值;
(3)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在锐角△ABC中,∠BAC≠60°,过点B、C分别作△ABC外接圆的切线BD、CE,且满足![]() ,直线DE与AB、AC的延长线分别交于点F、G、CF与BD交于点M,CE与BG交于点N.证明:
,直线DE与AB、AC的延长线分别交于点F、G、CF与BD交于点M,CE与BG交于点N.证明:![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com