分析:(1)要证AA
1⊥BC
1.只需证AA
1⊥面BDC
1,只需证AA
1垂直于面BDC
1内的两条相交直线,设AA
1中点为D,根据A
1B=AB,可得BD⊥AA
1,利用侧面ABB
1A
1⊥AA
1C
1C,可得BD⊥面AA
1C
1C.根据△ACC
1为正三角形,AC
1=C
1A
1,可得C
1D⊥AA
1,从而得证;
(2)由(1),有BD⊥C
1D,BC
1⊥CC
1,CC
1⊥面C
1DB,设点A
1到平面ABC的距离为h,利用等面积有
hS△ABC=VB-CAC1=VB-CDC1=
VC-C1DB,从而可求点A
1到平面ABC的距离.
解答: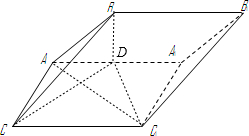
(1)证明:设AA
1中点为D,连BD,CD,C
1D,AC
1.
因为A
1B=AB,所以BD⊥AA
1.--------------------------2分
因为侧面ABB
1A
1⊥AA
1C
1C,所以BD⊥面AA
1C
1C.----------4分
又△ACC
1为正三角形,AC
1=C
1A
1,所以C
1D⊥AA
1.------6分
所以AA
1⊥面BDC
1,
所以AA
1⊥BC
1.----------------------------8分
(2)解:由(1),有BD⊥C
1D,BC
1⊥CC
1,CC
1⊥面C
1DB
设点A
1到平面ABC的距离为h,则
hS△ABC=VB-CAC1=VB-CDC1=
VC-C1DB.
因为
BD=C1D=,CC
1=1
∴
VC-C1DB=CC1×S△C1DB=
,
∵
CC1=1,BC1=,
∴
BC=∵AB=AC=1,
∴
S△ABC=∴
h=.
即点A
1到平面ABC的距离为
.----14分
点评:本题以三棱柱为载体,考查线面垂直的判定与性质,考查点面距离的求法,解题的关键是转换底面,利用体积相等求解.

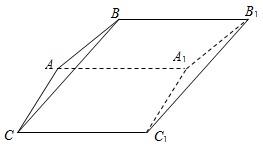 如图,斜三棱柱ABC-A1B1C1中,面AA1C1C是菱形,∠ACC1=60°,侧面ABB1A1⊥AA1C1C,A1B=AB=AC=1.求证:
如图,斜三棱柱ABC-A1B1C1中,面AA1C1C是菱形,∠ACC1=60°,侧面ABB1A1⊥AA1C1C,A1B=AB=AC=1.求证: (1)证明:设AA1中点为D,连BD,CD,C1D,AC1.
(1)证明:设AA1中点为D,连BD,CD,C1D,AC1.

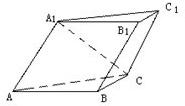 已知如图,斜三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2
已知如图,斜三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2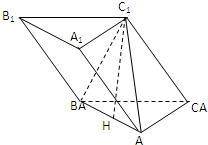 如图,斜三棱柱ABC-A1B1C1中,A1C1⊥BC1,AB⊥AC,AB=3,AC=2,侧棱与底面成60°角.
如图,斜三棱柱ABC-A1B1C1中,A1C1⊥BC1,AB⊥AC,AB=3,AC=2,侧棱与底面成60°角.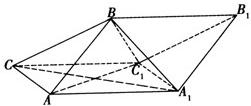 如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是面积为
如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是面积为 如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,AC⊥CB,∠ABC=45°,侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E、F分别是AB1、BC的中点.
如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,AC⊥CB,∠ABC=45°,侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E、F分别是AB1、BC的中点. (2012•潍坊二模)如图,斜三棱柱ABC-A1B1C1,侧面BB1C1C⊥底面ABC,△BC1C是等边三角形,AC⊥BC,AC=BC=4.
(2012•潍坊二模)如图,斜三棱柱ABC-A1B1C1,侧面BB1C1C⊥底面ABC,△BC1C是等边三角形,AC⊥BC,AC=BC=4.