
【题目】如图,在三棱柱![]() 中,面
中,面![]() 为矩形,
为矩形,![]() 为
为![]() 的中点,
的中点,![]() 与
与![]() 交于点
交于点![]() .
.
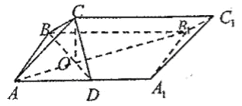
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]() ,求四面体AA1BC的体积.
,求四面体AA1BC的体积.
【答案】(1)证明略(2)![]()
【解析】
试题解析:(Ⅰ)证明:由已知得,![]() , ∴Rt△BAD∽Rt△ABB1
, ∴Rt△BAD∽Rt△ABB1
∴∠BDA=∠B1AB, ∴∠ABD+∠B1AB=∠ABD+∠BDA=90
∴在△AOB中,∠AOB=180 -(∠ABO+∠OAB ) =90,即BD⊥AB1
另BC⊥AB1,BD∩BC=B,∴AB1⊥平面BCD,CD![]() 平面BCD,
平面BCD,
∴CD⊥AB1
(Ⅱ) 在Rt△ABD中,AB=1,AD=![]() ∴AO=
∴AO=![]()
在Rt△AOB中, 得BO=![]() ,
,
在△BOC中,BO2+CO2=BC2 ,∴△BOC为直角三角形,
∴CO⊥BO, 由(1)易知,平面BCD⊥平面AA1B1B,平面BCD∩平面AA1B1B=BD
∴CO⊥平面AA1B1B,
∴四面体AA1BC的体积V=![]() S△AA1B
S△AA1B![]() OC=
OC=![]()
![]()
![]()
![]() 1
1![]()
![]()
![]()
![]() =
=![]()


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】某公司为了了解一年内的用水情况,抽取了10天的用水量如下表所示:
天数 | 1 | 1 | 1 | 2 | 2 | 1 | 2 |
用水量/吨 | 22 | 38 | 40 | 41 | 44 | 50 | 95 |
(Ⅰ)在这10天中,该公司用水量的平均数是多少?每天用水量的中位数是多少?
(Ⅱ)你认为应该用平均数和中位数中的哪一个数来描述该公司每天的用水量?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
已知平面直角坐标系![]() ,以
,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,
轴的非负半轴为极轴建立极坐标系,![]() 点的极坐标为
点的极坐标为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为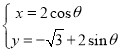 (
(![]() 为参数).
为参数).
(1)写出点![]() 的直角坐标及曲线
的直角坐标及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 中点
中点![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
:![]() ,半径为2的圆
,半径为2的圆![]() 与
与![]() 相切,圆心
相切,圆心![]() 在
在![]() 轴上且在直线
轴上且在直线![]() 的右上方.
的右上方.
(1)求圆的方程;
(2)若直线过点![]() 且与圆
且与圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 轴上方,
轴上方,![]() 在
在![]() 轴下方),问在
轴下方),问在![]() 轴正半轴上是否存在定点
轴正半轴上是否存在定点![]() ,使得
,使得![]() 轴平分
轴平分![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是公差为3的等差数列,数列{bn}是b1=1的等比数列,且![]() .
.
(Ⅰ)分别求数列{an},{bn}的通项公式;
(Ⅱ)令cn= an bn,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(I)求证:![]() 在区间
在区间![]() 上单调递增;
上单调递增;
(II)若![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,求
,求![]() 的试题分析式.并判断
的试题分析式.并判断![]() 是否有最大值和最小值,请说明理由(参考数据:
是否有最大值和最小值,请说明理由(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保护环境,2015年合肥市胜利工厂在市政府的大力支持下,进行技术改进:把二氧化碳转化为某种化工产品,经测算,该处理成本![]() (万元)与处理量
(万元)与处理量![]() (吨)之间的函数关系可近似地表示为:
(吨)之间的函数关系可近似地表示为: 且每处理一吨二氧化碳可得价值为20万元的某种化工产品.
且每处理一吨二氧化碳可得价值为20万元的某种化工产品.
(1)当![]() 时,判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不亏损?
时,判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不亏损?
(2)当处理量为多少吨时,每吨的平均处理成本最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com