
【题目】![]() 是指大气中空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国
是指大气中空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国![]() 标准采用世界卫生组织设定的最宽限值,即
标准采用世界卫生组织设定的最宽限值,即![]() 日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某城市环保局从该市市区2017年上半年每天的
日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某城市环保局从该市市区2017年上半年每天的![]() 监测数据中随机抽取18天的数据作为样本,将监测值绘制成茎叶图如下图所示(十位为茎,个位为叶).
监测数据中随机抽取18天的数据作为样本,将监测值绘制成茎叶图如下图所示(十位为茎,个位为叶).

(1)求这18个数据中不超标数据的平均数与方差;
(2)在空气质量为一级的数据中,随机抽取2个数据,求其中恰有一个为![]() 日均值小于30微克/立方米的数据的概率;
日均值小于30微克/立方米的数据的概率;
(3)以这![]() 天的
天的![]() 日均值来估计一年的空气质量情况,则一年(按
日均值来估计一年的空气质量情况,则一年(按![]() 天计算)中约有多少天的空气质量超标.
天计算)中约有多少天的空气质量超标.
【答案】(1)40,133;(2)![]() ;(3)160
;(3)160
【解析】试题分析:(1)根据茎叶图中的数据,利用定义即可求空气质量为不超标的数据的平均数与方差;(2)根据古典概型的概率公式即可求出恰有一个为![]() 日均值小于30微克/立方米的数据的概率;(3)求出空气质量超标的频率,即可得到结论.
日均值小于30微克/立方米的数据的概率;(3)求出空气质量超标的频率,即可得到结论.
试题解析:(1)空气质量为不超标数据有10个:26,27,33,34,36,39,42,43,55,65.
∴均值![]()
![]() ,方差
,方差![]() .
.
(2)由题目条件可知,空气质量为一级的数据共有4个,分别为26,27,33,34.
则由一切可能的结果组成的基本事件空间为![]() = {(26,27),(26,33),(26,34),(27,33),(27,34),(33,34)},共由6个基本事件组成.
= {(26,27),(26,33),(26,34),(27,33),(27,34),(33,34)},共由6个基本事件组成.
设“其中恰有一个为![]() 日均值小于30微克/立方米的数据
日均值小于30微克/立方米的数据![]() ”为事件A,
”为事件A,
则![]() ={(26,33),(26,34),(27,33),(27,34)},共有4个基本事件
={(26,33),(26,34),(27,33),(27,34)},共有4个基本事件
所以![]() .
.
(3)由题意,一年中空气质量超标的概率![]() ,
,![]() ,所以一年(按
,所以一年(按![]() 天计算)中约有
天计算)中约有![]() 天的空气质量超标.
天的空气质量超标.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】3名男生、3名女生站成一排:
(1)女生都不站在两端,有多少不同的站法?
(2)三名男生要相邻,有多少种不同的站法?
(3)三名女生互不相邻,三名男生也互不相邻,有多少种不同的站法?
(4)女生甲,女生乙都不与男生丙相邻,有多少种不同的站法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且函数
,且函数![]() 是偶函数,设
是偶函数,设![]()
(1)求![]() 的解析式;
的解析式;
(2)若不等式![]() ≥0在区间(1,e2]上恒成立,求实数
≥0在区间(1,e2]上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若方程![]() 有三个不同的实数根,求实数
有三个不同的实数根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分) 某居民小区有两个相互独立的安全防范系统(简称系统)![]() 和
和![]() ,系统
,系统![]() 和
和![]() 在任意时刻发生故障的概率分别为
在任意时刻发生故障的概率分别为![]() 和
和![]() 。
。
(Ⅰ)若在任意时刻至少有一个系统不发生故障的概率为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)设系统![]() 在3次相互独立的检测中不发生故障的次数为随机变量
在3次相互独立的检测中不发生故障的次数为随机变量![]() ,求
,求![]() 的概率分布列及数学期望
的概率分布列及数学期望![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校全体教师年龄的频率分布表如表1所示,其中男教师年龄的频率分布直方图如图2所示.已知该校年龄在![]() 岁以下的教师中,男女教师的人数相等.
岁以下的教师中,男女教师的人数相等.
表1:

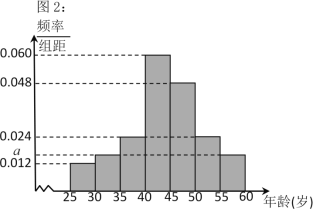
(1)求图2中![]() 的值;
的值;
(2)若按性别分层抽样,随机抽取16人参加技能比赛活动,求男女教师抽取的人数;
(3)若从年龄在![]() 的教师中随机抽取2人,参加重阳节活动,求至少有1名女教师的概率.
的教师中随机抽取2人,参加重阳节活动,求至少有1名女教师的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快餐连锁店招聘外卖骑手,该快餐连锁店提供了两种日工资方案:方案(1)规定每日底薪50元,快递业务每完成一单提成3元;方案(2)规定每日底薪100元,快递业务的前44单没有提成,从第45单开始,每完成一单提成5元.该快餐连锁店记录了每天骑手的人均业务量.现随机抽取100天的数据,将样本数据分为[ 25,35),[35,45),[45,55),[55,65),[65,75),[75,85),[85,95]七组,整理得到如图所示的频率分布直方图。
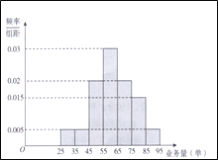
(1)随机选取一天,估计这一天该连锁店的骑手的人均日快递业务量不少于65单的概率;
(2)若骑手甲、乙选择了日工资方案(1),丙、丁选择了日工资方案(2).现从上述4名骑手中随机选取2人,求至少有1名骑手选择方案(1)的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=emx﹣lnx﹣2.
(1)若m=1,证明:存在唯一实数t∈( ![]() ,1),使得f′(t)=0;
,1),使得f′(t)=0;
(2)求证:存在0<m<1,使得f(x)>0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com