
【题目】已知函数![]()
(1)若![]() ,证明
,证明![]() ;
;
(2)若![]() ,求
,求![]() 的取值范围;并证明此时
的取值范围;并证明此时![]() 的极值存在且与
的极值存在且与![]() 无关.
无关.
【答案】(1)见解析(2)见解析
【解析】试题分析:
(1)利用题意求解导函数,求解![]() 得到函数的单调递增区间,求解
得到函数的单调递增区间,求解![]() 得到函数的单调递减区间,由
得到函数的单调递减区间,由![]() 可以得出结论;
可以得出结论;
(2)将![]() 变形为
变形为![]() ,构造函数
,构造函数![]() 结合函数的性质即可求得实数
结合函数的性质即可求得实数![]() 的取值范围;分类讨论
的取值范围;分类讨论![]() 和
和![]() 两种情况即可证明此时
两种情况即可证明此时![]() 的极值存在且与
的极值存在且与![]() 无关.
无关.
试题解析:
(1)若![]()
当![]() 单调递减;当
单调递减;当![]() 单调递增
单调递增
所以![]() ,得证
,得证
(1)若![]() ,变形得到
,变形得到![]() ,
,
令![]() ,得到
,得到![]()
![]() ,令
,令![]() ,可得
,可得![]() 在
在![]() 单增,在
单增,在![]() 单减,所以
单减,所以![]() ,
,
![]() 在
在![]() 单减,当
单减,当![]() 所以
所以![]() ,∴
,∴![]()
(注:若令![]() ),得到
),得到![]()
令![]() ,
,
![]() ,所以在
,所以在![]() 单减,在
单减,在![]() 单增,所以
单增,所以![]() ,
,
即![]() 在
在![]() 单增,当
单增,当![]() 所以
所以![]() ,∴
,∴![]()
下面再证明![]() 的极值存在且与
的极值存在且与![]() 无关:
无关:
①![]() ,
, ![]()
与![]() 无关.
无关.
②![]()
(其中 )所以
)所以![]() 且
且![]() 在
在![]() 处取极小值
处取极小值
![]()
因为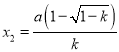 ,∴
,∴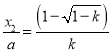 是关于
是关于![]() 的函数(与
的函数(与![]() 无关),
无关),
所以![]() 也是关于
也是关于![]() 的函数(与
的函数(与![]() 无关).
无关).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】经销商经销某种农产品,在一个销售季度内,每售出![]() 该产品获利润500元,未售出的产品,每
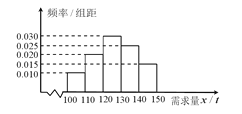
该产品获利润500元,未售出的产品,每![]() 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了
亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了![]() 该农产品.以
该农产品.以![]() (
(![]() )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量, ![]() (单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:元)表示下一个销售季度内经销该农产品的利润.
(Ⅰ)将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)根据直方图估计利润![]() 不少于57000元的概率.
不少于57000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知动直线![]() 过点
过点![]() ,且与圆
,且与圆![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)若直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的面积;
的面积;
(2)若直线![]() 的斜率为
的斜率为![]() ,点
,点![]() 是圆
是圆![]() 上任意一点,求
上任意一点,求![]() 的取值范围;
的取值范围;
(3)是否存在一个定点![]() (不同于点
(不同于点![]() ),对于任意不与
),对于任意不与![]() 轴重合的直线
轴重合的直线![]() ,都有
,都有![]() 平分
平分![]() ,若存在,求出定点
,若存在,求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
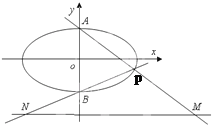
【题目】如图,已知椭圆![]() 的上、下顶点分别为A,B,点P在椭圆上,且异于点A,B,直线AP,BP与直线
的上、下顶点分别为A,B,点P在椭圆上,且异于点A,B,直线AP,BP与直线![]() 分别交于点M,N,
分别交于点M,N,
(1)设直线AP,BP的斜率分别为![]() ,求证:
,求证: ![]() 为定值;
为定值;
(2)求线段MN的长的最小值;
(3)当点P运动时,以MN为直径的圆是否经过某定点?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的顶点A(5,1),AB边上的中线CM所在直线方程为2x﹣y﹣5=0,AC边上的高BH所在直线方程为x﹣2y﹣5=0.求:
(1)顶点C的坐标;
(2)直线BC的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AA1⊥底面ABC,∠BAC=90°,AB=AC=2, ![]() .M,N分别为BC和CC1的中点,P为侧棱BB1上的动点.
.M,N分别为BC和CC1的中点,P为侧棱BB1上的动点. 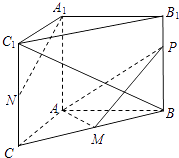
(1)求证:平面APM⊥平面BB1C1C;
(2)若P为线段BB1的中点,求证:A1N∥平面APM;
(3)试判断直线BC1与平面APM是否能够垂直.若能垂直,求PB的值;若不能垂直,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】京剧是我国的国粹,是“国家级非物质文化遗产”,某机构在网络上调查发现各地京剧票友的年龄![]() 服从正态分布
服从正态分布![]() 同时随机抽取
同时随机抽取![]() 位参与某电视台《我爱京剧》节目的票友的年龄作为样本进行分析研究(全部票友的年龄都在
位参与某电视台《我爱京剧》节目的票友的年龄作为样本进行分析研究(全部票友的年龄都在![]() 内),样本数据分别区间为
内),样本数据分别区间为![]() 由此得到如图所示的频率分布直方图.
由此得到如图所示的频率分布直方图.

(Ⅰ) 若![]() 求
求![]() 的值;
的值;
(Ⅱ)现从样本年龄在![]() 的票友中组织了一次有关京剧知识的问答,每人回答一个问题,答对赢得一台老年戏曲演唱机,答错没有奖品,假设每人答对的概率均为
的票友中组织了一次有关京剧知识的问答,每人回答一个问题,答对赢得一台老年戏曲演唱机,答错没有奖品,假设每人答对的概率均为![]() ,且每个人回答正确与否相互之间没有影响,用
,且每个人回答正确与否相互之间没有影响,用![]() 表示票友们赢得老年戏曲演唱机的台数,求
表示票友们赢得老年戏曲演唱机的台数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 为线段
为线段![]() 上的点,
上的点,
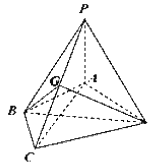
(1)证明: ![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,求
的中点,求![]() 与平面
与平面![]() 所成的角的正切值;
所成的角的正切值;
(3)若![]() 满足
满足![]() 面
面![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com