
分析 (1)运用数列的求和方法:分组求和,结合等比数列和等差数列的求和公式,计算即可得到所求和;
(2)运用反证法,假设{an}是等比数列,由定义,设公比为q,化简整理推出B=0与题意矛盾,即可得证;
(3)数列{an}中除去开始的两项之外,假设还有相等的两项,由题意可得B=-12A,构造函数f(x)=4x-12x,x>0,求出导数和单调性,即可得到结论.
解答 解:(1)由an=4n+n,
可得{an}的前n项之和为(4+42+…+4n)+(1+2+…+n)
=$\frac{4(1-{4}^{n})}{1-4}$+$\frac{1}{2}$n(n+1)=$\frac{4}{3}$(4n-1)+$\frac{1}{2}$(n2+n);
(2)证明:假设{an}是等比数列,
即有$\frac{{a}_{n+1}}{{a}_{n}}$=q(q为公比),
即为Aq•4n+Bq•n=A•4n+1+B•(n+1),
即Aq=4A,Bq=B,B=0,
解得q=4,B=0,这与B≠0矛盾,
则{an}不是等比数列;
(3)若a1=a2,数列{an}中除去开始的两项之外,假设还有相等的两项,
设为ak=am,(k,m不相等),
由a1=a2,可得4A+B=16A+2B,
即B=-12A.
则an=A•4n+B•n=A(4n-12•n),
即有A(4k-12•k)=A(4m-12•m),
即为4k-12•k=4m-12•m,
构造函数f(x)=4x-12x,x>0,
f′(x)=4xln4-12,
由f′(x)=0可得x0=log4$\frac{12}{ln4}$∈(1,2),
当x>x0时,f′(x)>0,f(x)递增,
故数列{an}中除去开始的两项之外,再没有相等的两项.
点评 本题考查数列的求和方法:分组求和,考查等比数列和等差数列的求和公式,同时考查反证法的运用,以及构造函数法,考查化简整理的运算能力,属于中档题.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:选择题
| 条件 | 方程 |
| ①△ABC周长为10 | C1:y2=25 |
| ②△ABC面积为10 | C2:x2+y2=4(y≠0) |
| ③△ABC中,∠A=90° | C3:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1(y≠0) |
| A. | C3,C1,C2 | B. | C1,C2,C3 | C. | C3,C2,C1 | D. | C1,C3,C2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
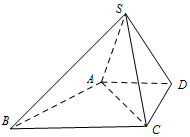 如图,在底面为直角梯形的四棱锥S-ABCD中,且AD∥BC,AD=DC=1,$SA=SC=SD=\sqrt{2}$.
如图,在底面为直角梯形的四棱锥S-ABCD中,且AD∥BC,AD=DC=1,$SA=SC=SD=\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
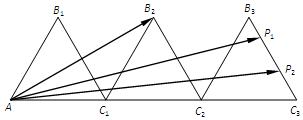 如图,△AB1C1,△C1B2C2,△C2B3C3是三个边长为2的等边三角形,且有一条边在同一直线上,边B3C3上有2个不同的点P1,P2,则$\overrightarrow{A{B_2}}•(\overrightarrow{A{P_1}}+\overrightarrow{A{P_2}})$=36.
如图,△AB1C1,△C1B2C2,△C2B3C3是三个边长为2的等边三角形,且有一条边在同一直线上,边B3C3上有2个不同的点P1,P2,则$\overrightarrow{A{B_2}}•(\overrightarrow{A{P_1}}+\overrightarrow{A{P_2}})$=36.查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高二文下学期期末考试数学试卷(解析版) 题型:选择题
已知定义在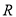 上的函数
上的函数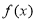 为单调函数,且对任意
为单调函数,且对任意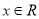 ,恒有
,恒有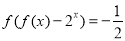 ,若
,若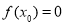 ,则
,则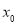 的值是( )
的值是( )
A.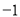 B.
B.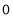 C.
C.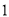 D.
D.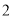
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com