
【题目】已知函数f(x)=xlnx.
(1)求f(x)的单调区间和极值;
(2)设A(x1 , f(x1)),B(x2 , f(x2)),且x1≠x2 , 证明: ![]() <f′(
<f′( ![]() ).
).
【答案】
(1)解:定义域为(0,+∞),f′(x)=lnx+x ![]() =1+lnx,
=1+lnx,
令f′(x)>0,则lnx>﹣1=ln ![]() ,∴x>
,∴x> ![]() ;
;
令f′(x)<0,则lnx<﹣1=ln ![]() ,∴0<x<
,∴0<x< ![]() ,
,
∴f(x)的单调增区间是( ![]() ,+∞),单调减区间是(0,
,+∞),单调减区间是(0, ![]() ).
).
f(x)极小值=f( ![]() )=
)= ![]() =﹣
=﹣ ![]() ,f(x)无极大值
,f(x)无极大值
(2)证明:不妨设x1<x2,
![]()
![]() <ln
<ln ![]() +1,即
+1,即 ![]() ﹣
﹣ ![]() +x2﹣x1,
+x2﹣x1,
![]() <
< ![]() ,
,
两边同除以x1得, ![]()
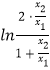 <ln
<ln 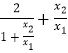 ﹣1,
﹣1,
令 ![]() =t,则t>1,即证:tln
=t,则t>1,即证:tln ![]() <ln
<ln ![]() +t﹣1,
+t﹣1,
令g(t)=tln ![]() ﹣t+1,
﹣t+1,
g′(t)=ln ![]() +t
+t ![]() +
+ ![]() ﹣1=ln
﹣1=ln ![]() =ln(1+
=ln(1+ ![]() )﹣
)﹣ ![]() ,
,
令 ![]() (x>0),h(x)=ln(1+x)﹣x,
(x>0),h(x)=ln(1+x)﹣x,
h′(x)= ![]() <0,h(x)在(0,+∞)上单调递减,
<0,h(x)在(0,+∞)上单调递减,
∴h(x)<h(0)=0,即ln(1+x)<x,即g′(t)=ln(1+ ![]() )﹣
)﹣ ![]() <0恒成立,
<0恒成立,
∴g(t)在(1,+∞)上是减函数,所以g(t)<g(1)=0,
∴tln ![]() <ln
<ln ![]() +t﹣1得证,
+t﹣1得证,
∴ ![]() 成立
成立
【解析】(1)求导,在定义域内解不等式f′(x)>0,f′(x)<0可得单调区间,有极值点的定义可求极值;(2)不妨设x1<x2 , ![]()
![]() <ln
<ln ![]() +1,即证
+1,即证 ![]() <
< ![]() ,两边同除以x1得,
,两边同除以x1得, ![]()
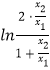 <ln
<ln 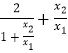 ﹣1,令
﹣1,令 ![]() =t,则t>1,只证:tln
=t,则t>1,只证:tln ![]() <ln
<ln ![]() +t﹣1,令g(t)=tln
+t﹣1,令g(t)=tln ![]() ﹣t+1,利用导数证明g(t)<0即可;
﹣t+1,利用导数证明g(t)<0即可;
【考点精析】利用利用导数研究函数的单调性和函数的最大(小)值与导数对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


科目:高中数学 来源: 题型:
【题目】唐三彩,中国古代陶瓷烧制工艺的珍品,它吸取了中国国画、雕塑等工艺美术的特点,在中国文化中占有重要的历史地位,在中国的陶瓷史上留下了浓墨重彩的一笔,唐三彩的生产至今已有1300多年的历史,对唐三彩的复制和仿制工艺,至今也有百余年的历史.某陶瓷厂在生产过程中,对仿制的100件工艺品测得其重量(单位;kg)数据,将数据分组如下表:

(1)在答题卡上完成频率分布表;
(2)重量落在![]() 中的频率及重量小于2.45的频率是多少?
中的频率及重量小于2.45的频率是多少?
(3)统计方法中,同一组数据常用该组区间的中点值(例如区间![]() 的中点值是
的中点值是![]() 作为代表.据此,估计这100个数据的平均值.
作为代表.据此,估计这100个数据的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当前,网购已成为现代大学生的时尚。某大学学生宿舍4人参加网购,约定:每个人通过掷一枚质地均匀的骰子决定自己去哪家购物,掷出点数为5或6的人去淘宝网购物,掷出点数小于5的人去京东商城购物,且参加者必须从淘宝网和京东商城选择一家购物.
(1)求这4个人中恰有1人去淘宝网购物的概率;
(2)用![]() 分别表示这4个人中去淘宝网和京东商城购物的人数,记
分别表示这4个人中去淘宝网和京东商城购物的人数,记![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】P为圆C1:x2+y2=9上任意一点,Q为圆C2:x2+y2=25上任意一点,PQ中点组成的区域为M,在C2内部任取一点,则该点落在区域M上的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)判定f(x)的奇偶性并证明;
(Ⅲ)用函数单调性定义证明:f(x)在(1,+∞)上是增函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人要对C处进行考察,甲在A处,乙在B处,基地在O处,此时∠AOB=90°,测得|AC|=5 km,|BC|=![]() km,|AO|=|BO|=2 km,如图所示,试问甲、乙两人应以什么方向走,才能使两人的行程之和最小?
km,|AO|=|BO|=2 km,如图所示,试问甲、乙两人应以什么方向走,才能使两人的行程之和最小?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥ABCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别为AD,BC的中点,则异面直线AN,CM所成的角的余弦值是( ) 
A.![]()
B.﹣ ![]()
C.﹣ ![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆C1: ![]() =1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是
=1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是 ![]() .
. 
(1)求椭圆C1的标准方程;
(2)过F作直线l交抛物线C2于A,B两点,过F且与直线l垂直的直线交椭圆C1于另一点C,求△ABC面积的最小值,以及取到最小值时直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com