
【题目】下列说法正确的是 ( )
A. “若![]() ,则
,则![]() ,或
,或![]() ”的否定是“若
”的否定是“若![]() 则
则![]() ,或
,或 ![]() ”
”
B. a,b是两个命题,如果a是b的充分条件,那么![]() 是
是![]() 的必要条件.
的必要条件.
C. 命题“![]() ,使 得
,使 得![]() ”的否定是:“
”的否定是:“![]() ,均有
,均有 ![]() ”
”
D. 命题“ 若![]() ,则
,则![]() ”的否命题为真命题.
”的否命题为真命题.
科目:高中数学 来源: 题型:
【题目】斜率为k的直线l经过抛物线y=![]() x2的焦点F,且与抛物线相交于A,B两点,若线段|AB|的长为8.
x2的焦点F,且与抛物线相交于A,B两点,若线段|AB|的长为8.
(1)求抛物线的焦点F的坐标和准线方程;
(2)求直线的斜率k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() ,
,![]() ),记函数
),记函数![]() 的导函数为
的导函数为![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)是否存在实数![]() ,使得
,使得![]() 对任意正实数
对任意正实数![]() 恒成立?若存在,求出满足条件的实数
恒成立?若存在,求出满足条件的实数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以平面直角坐标系
为参数),以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 上的动点
上的动点![]() 到坐标原点
到坐标原点![]() 的距离
的距离![]() 的最大值;
的最大值;
(Ⅱ)若曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且与
两点,且与![]() 轴相交于点
轴相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系![]() 中,平行于
中,平行于![]() 轴且过点
轴且过点![]() 的入射光线
的入射光线![]() 被直线
被直线![]() 反射,反射光线
反射,反射光线![]() 交
交![]() 轴于
轴于![]() 点,圆
点,圆![]() 过点
过点![]() ,且与
,且与![]() 、
、![]() 相切.
相切.
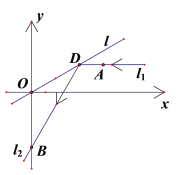
(Ⅰ)求![]() 所在直线的方程;
所在直线的方程;
(Ⅱ)求圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】语文中有回文句,如:“上海自来水来自海上”,倒过来读完全一样。数学中也有类似现象,如:88,454,7337,43534等,无论从左往右读,还是从右往左读,都是同一个数,称这样的数为“回文数”!
二位的回文数有11,22,33,44,55,66,77,88,99,共9个;
三位的回文数有101,111,121,131,…,969,979,989,999,共90个;
四位的回文数有1001,1111,1221,…,9669,9779,9889,9999,共90个;
由此推测:11位的回文数总共有_________个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为研究冬季昼夜温差大小对某反季节大豆新品种发芽率的影响,某校课外兴趣小组记录了![]() 组昼夜温差与
组昼夜温差与![]() 颗种子发芽数,得到如下资料:
颗种子发芽数,得到如下资料:
组号 | 1 | 2 | 3 | 4 | 5 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
经分析,这组数据具有较强的线性相关关系,因此该小组确定的研究方案是:先从这五组数据中选取![]() 组数据求出线性回归方程,再用没选取的
组数据求出线性回归方程,再用没选取的![]() 组数据进行检验.
组数据进行检验.
(1)若选取的是第![]() 组的数据,求出
组的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过![]() 颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
(参考公式: ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在D上的函数f(x),如果满足对任意x∈D,存在常数M>0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的上界,已知函数f(x)=1+x+ax2
(1)当a=﹣1时,求函数f(x)在(﹣∞,0)上的值域,判断函数f(x)在(﹣∞,0)上是否为有界函数,并说明理由;
(2)若函数f(x)在x∈[1,4]上是以3为上界的有界函数,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com