
某地区对12岁儿童瞬时记忆能力进行调查.瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学甲、乙两人参加一次英语口语考试,已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题.规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才算合格.(1)求甲、乙两人考试均合格的概率;(2)求甲答对试题数 的概率分布及数学期望.
的概率分布及数学期望.
(1) ;
;
(2)ξ 0 1 2 3 P 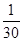
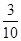
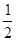
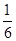
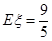
解析试题分析:(1)每人参加考试合格,必须且只需从备选的10个题中随机抽出3题进行测试,至少答对2题才算合格,即恰好答对2题或恰好答对3题,由已知及古典型概率公式可求出甲、乙两人考试分别合格的概率,且知两人参加考试合格的事件是相互独立的,从而由相互独立事件同时发生的概率积公式可求得甲、乙两人考试均合格的概率;(2)由于每次考试都从备选题中随机抽出3题进行测试,故甲答对试题数 的所有可能取值只可能是:0,1,2,3.不可能再有第四种可能了,应用古典型概率计算公式,可计算出
的所有可能取值只可能是:0,1,2,3.不可能再有第四种可能了,应用古典型概率计算公式,可计算出 的每一个取值对应事件的概率,从而得到甲答对试题数ξ的概率分布及数学期望.
的每一个取值对应事件的概率,从而得到甲答对试题数ξ的概率分布及数学期望.
试题解析:(1)设甲、乙两人考试合格的事件分别为A、B,则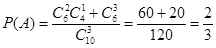 ,
,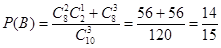 ;因为事件A、B相互独立,所以甲、乙两人考试均合格的概率为:
;因为事件A、B相互独立,所以甲、乙两人考试均合格的概率为: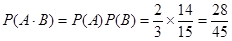 .答:甲、乙两人考试均合格的概率为
.答:甲、乙两人考试均合格的概率为 .
.
(2)依题意,知 的所有可能取值为:0,1,2,3.则
的所有可能取值为:0,1,2,3.则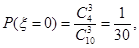
 ,
,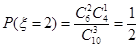 ,
,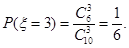
甲答对试题数ξ的概率分布如下:ξ 0 1 2 3 P 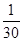
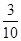
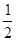
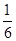
甲答对试题数ξ的数学期望 12分
12分
考点:1.古典概率;2.随机变量的分布列;3.数学期望.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:解答题
在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为x、y,记ξ=|x-2|+|y-x|.
(1)求随机变量ξ的最大值,并求事件“ξ取得最大值”的概率;
(2)求随机变量ξ的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个均匀的正方体玩具,各个面上分别写有1,2,3,4,5,6,将这个玩具先后抛掷2次,求:
(1)朝上的一面数相等的概率;(2)朝上的一面数之和小于5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知方程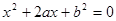 是关于
是关于 的一元二次方程.
的一元二次方程.
(1)若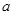 是从集合
是从集合 四个数中任取的一个数,
四个数中任取的一个数,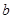 是从集合
是从集合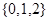 三个数中任取的一个数,求上述方程有实数根的概率;
三个数中任取的一个数,求上述方程有实数根的概率;
(2)若 ,
, ,求上述方程有实数根的概率.
,求上述方程有实数根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)将一颗骰子先后抛掷2次,观察向上的点数,求:
(1)两数之和为6的概率;
(2)两数之积是6的倍数的概率;
(3)以第一次向上点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)在圆x2+y2=15的内部的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)把一颗质地均匀,四个面上分别标有复数 ,
,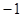 ,
,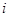 ,
,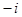 (
(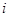 为虚数单位)的正四面体玩具连续抛掷两次,第一次出现底面朝下的复数记为
为虚数单位)的正四面体玩具连续抛掷两次,第一次出现底面朝下的复数记为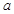 ,第二次出现底面朝下的复数记为
,第二次出现底面朝下的复数记为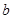 .
.
(1)用 表示“
表示“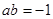 ”这一事件,求事件
”这一事件,求事件 的概率
的概率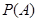 ;
;
(2)设复数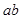 的实部为
的实部为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解某班关注NBA(美国职业篮球)是否与性别有关,对某班48人进行了问卷调查得到如下的列联表:
| | 关注NBA | 不关注NBA | 合计 |
| 男生 | | 6 | |
| 女生 | 10 | | |
| 合计 | | | 48 |
 .
.| P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com