
����Ŀ����һ���Ե�OΪԲ�ģ��뾶Ϊ2����Բ�β�ƺ����ƺ�ھ���O�� ![]() ����D����һ���ڹ�ȵ�ˮ��ͷ����������D��һ����ֱС·����ƺԲ����A��B���㣬Ϊ�˷������ɢ����ͬʱ��С·OA��OB������С·�Ŀ��Ⱥ��Բ��ƣ�
����D����һ���ڹ�ȵ�ˮ��ͷ����������D��һ����ֱС·����ƺԲ����A��B���㣬Ϊ�˷������ɢ����ͬʱ��С·OA��OB������С·�Ŀ��Ⱥ��Բ��ƣ�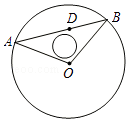
��1����Ҫʹ����С·�ķ�����ʡ������С·����̳��ȣ�
��2����Ҫ�ڡ�ABO�����ڣ����߽磩�滮��һ��Բ�εij����������������㳡�裬�������Բ�ι㳡����������������������źͦУ�
���𰸡�
��1���⣺С·�ij���l=OA+OB+AB=��400+AB���ף�
ҪʹС·�ij�����̣�ֻ��AB��̼��ɣ�
��OD��ABʱ��Բ�ľ�d�ΪOD����ʱAB��̣�
��AB��min=2 ![]() ��2=200
��2=200 ![]() �ף�
�ף�
��С·����̳���Ϊ��4+2 ![]() �������ף���
�������ף���
��2�������⣬Բ�ι㳡�����ڡ�ABOʱ�����Բ�ι㳡����������
���ABO������Բ�뾶Ϊr��
���� ![]() =
= ![]() ��
��
���ҳ���ʽ��AB=2 ![]() ��
�� ![]()
![]() ��
��
��AB=x����r2=f��x��= ![]() ��
�� ![]() ��
��
�� ![]() ����x=AB=2
����x=AB=2 ![]() ��
��
�� ![]() ����
���� ![]() =6��4
=6��4 ![]() ��
��
���Բ�ι㳡��������s=��r2=��6��4 ![]() ���У�����2��
��������2��
����������1����д��С·���ȵĺ�������ʽ���������ҳ���ʽ�ɵ�AB����Сֵ�������ɵ�С·����̳��ȣ���2������AB=x��������֪�����ɵ�r2�ú���x��ʽ�ӱ�ʾ������r2=f��x������f��x�����ж�f��x���ĵ����ԣ������ɵ�f��x�������ֵ���Ӷ��ɵ����Բ�ι㳡����������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() ������g��x��=f��f��x������2�����䣨��1��3]�ϵ��������ǣ�������
������g��x��=f��f��x������2�����䣨��1��3]�ϵ��������ǣ�������
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC�� ![]() ������
������ ![]() �����ҽ���ֱ�ΪF1��F2 �� Բx2+y2=2��ֱ��x+y+b=0�ཻ�����ҳ�Ϊ2��
�����ҽ���ֱ�ΪF1��F2 �� Բx2+y2=2��ֱ��x+y+b=0�ཻ�����ҳ�Ϊ2��
��������ԲC�ı����̣�
������Q����ԲC�ϲ���x���ϵ�һ�����㣬OΪ����ԭ�㣬����F2��OQ��ƽ���߽���ԲC��M��N������ͬ�ĵ�
����̽�� ![]() ��ֵ�Ƿ�Ϊһ�����������ǣ������������������ǣ���˵�����ɣ�
��ֵ�Ƿ�Ϊһ�����������ǣ������������������ǣ���˵�����ɣ�
�Ƽǡ�QF2M�����ΪS1 �� ��OF2N�����ΪS2 �� ��S=S1+S2 �� ��S�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�����P��0��1���һ��ഹֱ������ֱ�߷ֱ���
ԲO��x2+y2=4���ڵ�A��B����ԲM����x��2��2+��y��1��2=1���ڵ�C��D��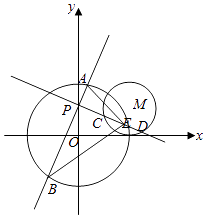
��1���� ![]() ����CD�ij���
����CD�ij���
��2����CD�е�ΪE�����ABE�����ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���ֱ֪��l����ͨ����Ϊx��y��2=0������C�IJ�������Ϊ ![]() ����Ϊ����������ֱ��l������C����A��B���㣮����P������C���˶�������PAB��������ʱ�����P�����꼰��PAB����������
����Ϊ����������ֱ��l������C����A��B���㣮����P������C���˶�������PAB��������ʱ�����P�����꼰��PAB����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�������֧��50��Ԫ����һ�����������һ������ɸ��ַ�����֧��6��Ԫ���ӵڶ�����ÿ�궼����һ������֧��2��Ԫ���ٶ��ó�ÿ������������Ϊ25��Ԫ��С���ڸó������ۼ����볬����֧�����ǽ��������Ϊ���ֳ����ۣ����ó��ڵ�x����׳��ۣ�����������Ϊ25��x��Ԫ�����ҹ涨������ı�������Ϊ10�꣩��
��1����������䵽�ڼ�����ף��ó������ۼ����볬����֧����
��2���ڵڼ��������������ۣ���ʹС�Ż�õ���ƽ�������������=�ۼ�����+�������멁��֧����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD��A1B1C1D1�У�����ADD1A1�͵���ABCD��D1A=D1D= ![]() ������ABCDΪֱ�����Σ�����BC��AD��AB��AD��AD=2AB=2BC=2��OΪAD�е㣮
������ABCDΪֱ�����Σ�����BC��AD��AB��AD��AD=2AB=2BC=2��OΪAD�е㣮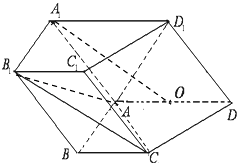
������֤��A1O��ƽ��AB1C��
������������A��C1D1��C������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������ȡ������ҵ�������Ͻ�˰�����{��λ��Ԫ�����������ݻ��Ƴ�Ƶ�ʷֲ�ֱ��ͼ����ͼ�������Ͻ�˰�շ�Χ��[0��100]�������ݷ���Ϊ[0��20����[20��40��[40��60��[60��80����[80��100��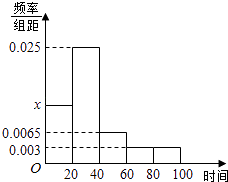
��1����ֱ��ͼ��x��ֵ��
��2��������Ͻ�˰�ղ�����60��Ԫ����ҵ�����������Żݣ�������ȡ��ҵ1200�����Թ����ж�����ҵ�������������Żݣ�
��3������ҵ����ѡ4������4����ҵ���Ͻ�˰������20��Ԫ�ĸ�����ΪX����X�ķֲ��к���ѧ��������ֱ��ͼ�е�Ƶ����Ϊ���ʣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com