
(14分)已知函数![]() ,且其导函数
,且其导函数![]() 的图像过原点.
的图像过原点.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的图像在
的图像在![]() 处的切线方程;
处的切线方程;
(Ⅱ)若存在![]() ,使得
,使得![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ)当![]() 时,求函数
时,求函数![]() 的零点个数.
的零点个数.
解析: ![]() ,
,![]()
由![]() 得
得 ![]() ,
,![]() .---------------------2分
.---------------------2分
(Ⅰ) 当![]() 时,
时, ![]() ,
,![]() ,
,![]() ,
,![]()
所以函数![]() 的图像在
的图像在![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() --------------------4分
--------------------4分
(Ⅱ) 存在![]() ,使得
,使得![]() ,
,
![]() ,
,![]() ,
,
当且仅当![]() 时,
时,![]()
所以![]() 的最大值为
的最大值为![]() . -----------------9分
. -----------------9分
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大值 |
| 极小值 |
|
(Ⅲ) 当![]() 时,
时,![]() 的变化情况如下表:
的变化情况如下表:
-
---11分
![]() 的极大值
的极大值![]() ,
,![]() 的极小值
的极小值![]()
又![]()
![]() ,
,![]() .
.
所以函数![]() 在区间
在区间![]() 内各有一个零点,
内各有一个零点,
故函数![]() 共有三个零点。--------------------14分
共有三个零点。--------------------14分
注:①证明![]() 的极小值
的极小值![]() 也可这样进行:
也可这样进行:
设![]() ,则
,则![]()
当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,函数
,函数![]() 在区间
在区间![]() 上是增函数,在区间
上是增函数,在区间![]() 上是减函数,故函数
上是减函数,故函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,从而
,从而![]() 的极小值
的极小值![]() .
.
②证明函数![]() 共有三个零点。也可这样进行:
共有三个零点。也可这样进行:
![]() 的极大值
的极大值![]() ,
,![]() 的极小值
的极小值![]() ,
,
当 ![]() 无限减小时,
无限减小时,![]() 无限趋于
无限趋于![]() 当
当 ![]() 无限增大时,
无限增大时,![]() 无限趋于
无限趋于![]()
故函数![]() 在区间
在区间![]() 内各有一个零点,
内各有一个零点,
故函数![]() 共有三个零点。--------------------14分
共有三个零点。--------------------14分


科目:高中数学 来源: 题型:
| f2(x2)-f2(x1) | x2-x1 |
查看答案和解析>>
科目:高中数学 来源:广东省惠州市2013届高三第一次调研考试数学文科试题 题型:044
已知函数![]() ,且其导函数
,且其导函数![]() 的图像过原点.
的图像过原点.
(1)当a=1时,求函数f(x)的图像在x=3处的切线方程;
(2)若存在x<0,使得![]() ,求a的最大值;
,求a的最大值;
(3)当a>0时,求函数f(x)的零点个数.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省高三8月摸底考试文科数学试卷(解析版) 题型:解答题
已知函数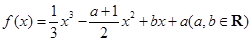 ,且其导函数
,且其导函数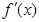 的图像过原点.
的图像过原点.
(1)当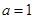 时,求函数
时,求函数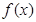 的图像在
的图像在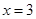 处的切线方程;
处的切线方程;
(2)若存在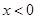 ,使得
,使得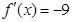 ,求
,求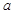 的最大值;
的最大值;
查看答案和解析>>
科目:高中数学 来源:模拟题 题型:解答题
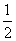 x2,g(x)=logax(a>0且a≠1),
x2,g(x)=logax(a>0且a≠1),查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com