
【题目】已知函数y=x+ ![]() 有如下性质:如果常数t>0,那么该函数在
有如下性质:如果常数t>0,那么该函数在 ![]() 上是减函数,在
上是减函数,在 ![]() 上是增函数.
上是增函数.
(1)已知f(x)= ![]() ,x∈[﹣1,1],利用上述性质,求函数f(x)的单调区间和值域;
,x∈[﹣1,1],利用上述性质,求函数f(x)的单调区间和值域;
(2)对于(1)中的函数f(x)和函数g(x)=﹣x﹣2a,若对任意x1∈[﹣1,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数a的值.
【答案】
(1)解:y= ![]() =x+2+
=x+2+ ![]() ﹣6;
﹣6;
设u=x+2,x∈[﹣1,1],1≤u≤3,u=x+2为增函数;
则y=u+ ![]() ﹣6,u∈[1,3];
﹣6,u∈[1,3];
由已知性质得,①当1≤u≤2,即﹣1≤x≤0时,f(x)单调递减;
∴f(x)的减区间为[﹣1,0];
②当2≤u≤3,即0≤x≤1时,f(x)单调递增;
∴f(x)的增区间为[0,1];
由f(﹣1)=﹣1,f(0)=﹣2,f(1)= ![]() ;
;
得f(x)的值域为[﹣2,﹣1]
(2)解:g(x)=﹣x﹣2a为减函数,x∈[0,1];
故g(x)∈[﹣1﹣2a,﹣2a];
由题意,f(x)的值域是g(x)的值域的子集;
∴ ![]() ;
;
∴ ![]() ;
;
即实数a的值为 ![]()
【解析】(1)根据条件,先变形f(x)= ![]() ,可令x+2=u,1≤u≤3,而函数u=x+2为增函数,从而根据复合函数的单调性及已知的性质便可得出f(x)的减区间为[﹣1,0],增区间为[0,1],进一步便可得出f(x)的值域为[﹣2,﹣1];(2)根据题意便知f(x)的值域为g(x)的子集,而容易求出g(x)的值域为[﹣1﹣2a,﹣2a],从而得出
,可令x+2=u,1≤u≤3,而函数u=x+2为增函数,从而根据复合函数的单调性及已知的性质便可得出f(x)的减区间为[﹣1,0],增区间为[0,1],进一步便可得出f(x)的值域为[﹣2,﹣1];(2)根据题意便知f(x)的值域为g(x)的子集,而容易求出g(x)的值域为[﹣1﹣2a,﹣2a],从而得出 ![]() ,这样即可得出实数a的值.
,这样即可得出实数a的值.
【考点精析】解答此题的关键在于理解函数单调性的判断方法的相关知识,掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较,以及对函数的值的理解,了解函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法.


科目:高中数学 来源: 题型:
【题目】某机构为了解某地区中学生在校月消费情况,随机抽取了100名中学生进行调查.如图是根据调查的结果绘制的学生在校月消费金额的频率分布直方图.已知[350,450),[450,550),[550,650)三个金额段的学生人数成等差数列,将月消费金额不低于550元的学生称为“高消费群”. 
(1)求m,n的值,并求这100名学生月消费金额的样本平均数 ![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)根据已知条件完成下面2×2列联表,并判断能否有90%的把握认为“高消费群”与性别有关?
高消费群 | 非高消费群 | 合计 | |
男 | |||
女 | 10 | 50 | |
合计 |
(参考公式: ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校学生社团为了解“大数据时代”下大学生就业情况的满意度,对20名学生进行问卷计分调查(满分100分),得到如图所示的茎叶图:
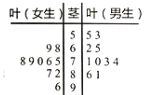
(1)计算男生打分的平均分,观察茎叶图,评价男女生打分的分散程度;
(2)从打分在80分以上的同学随机抽3人,求被抽到的女生人数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD= ![]() CD=a,PD=
CD=a,PD= ![]() a.
a. 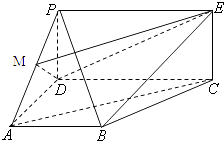
(1)若M为PA中点,求证:AC∥平面MDE;
(2)求平面PAD与PBC所成锐二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有这样一则问题:“今有良马与弩马发长安,至齐,齐去长安三千里,良马初日行一百九十三里,日增一十三里;弩马初日行九十七里,日减半里,良马先至齐,复还迎弩马.”则现有如下说法:
①弩马第九日走了九十三里路;
②良马前五日共走了一千零九十五里路;
③良马和弩马相遇时,良马走了二十一日.
则以上说法错误的个数是( )个
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】规定投掷飞镖3次为一轮,若3次中至少两次投中8环以上为优秀,现采用随机模拟实验的方法估计某人投掷飞镖的情况:先由计算器产生随机数0或1,用0表示该次投标未在8环以上,用1表示该次投标在8环以上;再以每三个随机数作为一组,代表一轮的结果,经随机模拟实验产生了如下20组随机数:
101 111 011 101 010 100 100 011 111 110
000 011 010 001 111 011 100 000 101 101
据此估计,该选手投掷飞镖三轮,至少有一轮可以拿到优秀的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1, ![]() 中,
中, ![]() ,点
,点![]() 为线段
为线段![]() 的四等分点,线段
的四等分点,线段![]() 互相平行,现沿
互相平行,现沿![]() 折叠得到图2所示的几何体,此几何体的底面
折叠得到图2所示的几何体,此几何体的底面![]() 为正方形.
为正方形.
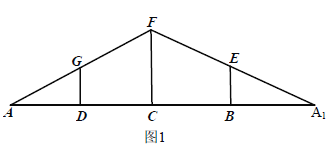

(1)证明: ![]() 四点共面;(2)求四棱锥
四点共面;(2)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为: ![]() (t为参数,其中0<α<
(t为参数,其中0<α< ![]() ),椭圆M的参数方程为
),椭圆M的参数方程为 ![]() (β为参数),圆C的标准方程为(x﹣1)2+y2=1.
(β为参数),圆C的标准方程为(x﹣1)2+y2=1.
(1)写出椭圆M的普通方程;
(2)若直线l为圆C的切线,且交椭圆M于A,B两点,求弦AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com