
【题目】设函数![]() ,函数
,函数![]() ,则方程
,则方程![]() 实数解的个数是( ).
实数解的个数是( ).
A.1个B.2个C.3个D.4个
【答案】C
【解析】
根据函数![]() 在
在![]() 上单调递增和在任意区间
上单调递增和在任意区间![]() ,
,![]() 上,函数
上,函数![]() 的值为定值得在任意区间
的值为定值得在任意区间![]() ,
,![]() 上,方程
上,方程![]() 至多有一个实数解,再分别对
至多有一个实数解,再分别对![]() 时,
时,![]() 时,
时,![]() 时,求得
时,求得![]() 的解,再运用数学归纳法证明
的解,再运用数学归纳法证明![]() ,
,![]() ,
,![]() 时,
时,![]() 恒成立,即
恒成立,即![]() 无解,从而得选项。
无解,从而得选项。
由题意知![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 时,
时,![]() 。
。
由对数函数性质知函数![]() 在
在![]() 上单调递增,
上单调递增,
由![]() ,
,![]() ,
,![]() 知:在任意区间
知:在任意区间![]() ,
,![]() 上,函数
上,函数![]() 的值为定值。
的值为定值。
则在任意区间![]() ,
,![]() 上,方程
上,方程![]() 至多有一个实数解。
至多有一个实数解。
①当![]() 时,
时,![]() ,令
,令![]() ,解得
,解得![]() ,
,
故此时![]() 有唯一解
有唯一解![]() ;
;
②当![]() 时,
时,![]() ,令
,令![]() ,解得
,解得![]() ,
,
故此时![]() 有唯一解
有唯一解![]() ;
;
③当![]() 时,
时,![]() ,令
,令![]() ,解得
,解得![]() ,
,
故此时![]() 有唯一解
有唯一解![]() ;
;
④当![]() 时,
时,![]() ,令
,令![]() ,解得
,解得![]() ,
,
故此时![]() 无解,因为
无解,因为![]() ,所以
,所以![]() 恒成立;
恒成立;
⑤设![]() ,
,![]() ,
,![]() 时,
时,![]() 恒成立,
恒成立,
而![]() ,
,![]() ,
,![]() 时,
时,![]() ,
,
则![]() 恒成立等同于
恒成立等同于![]() 恒成立,
恒成立,
当![]() ,
,![]() ,
,![]() 时,
时,
![]()
![]()
![]()
![]() ,
,
所以当![]() ,
,![]() ,
,![]() 时,则有
时,则有![]() 仍然恒成立。
仍然恒成立。
由④知![]() 时,即
时,即![]() 时,
时,![]() 恒成立,
恒成立,
则![]() ,
,![]() ,
,![]() 时,
时,![]() 恒成立,即
恒成立,即![]() 无解。
无解。
综上所述,方程![]() 的实数根为
的实数根为![]() ,
,![]() 以及
以及![]() ,共3个。
,共3个。
故选:C。


科目:高中数学 来源: 题型:
【题目】![]() 设a,b,c,d均为正数,且a+b=c+d,证明:(1)若ab > cd,则
设a,b,c,d均为正数,且a+b=c+d,证明:(1)若ab > cd,则 ![]() +
+![]() >
>![]() +
+ ![]() ;(2)
;(2) ![]() +
+![]() >
> ![]() +
+ ![]() 是|a-b| < |c-d|的充要条件
是|a-b| < |c-d|的充要条件
(1)(I)若ab![]() cd,则
cd,则![]() +
+![]()
![]()
![]() +
+![]()
(2)(II)![]() +
+![]()
![]()
![]() +
+![]() 是|a-b|
是|a-b|![]() |c-d|的充要条件
|c-d|的充要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
A.(1,3)
B.(1, 4)
C.(2,3)
D.(2,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)在直角坐标系xOy中,直线l的参数方程为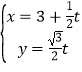 (t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,
(t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,![]() c的极坐标方程为
c的极坐标方程为![]() =2
=2![]() sin
sin![]() .
.
(1)写出![]() c的直角坐标方程;
c的直角坐标方程;
(2)P为直线l上一动点,当P到圆心C的距离最小时,求P的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)设△ABC的内角A,B,C的对边分别为a,b,c,a=btanA,
(1)证明:sinB=cosA
(2)若sinC-sinAcosB=![]() ,且B为钝角,求A,B,C
,且B为钝角,求A,B,C
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个二元码是由0和1组成的数字![]() 其中
其中![]() 称为第k位码元,二元码是通信中常用的码,但在通信过程中有时会发生码元错误(即码元由0变为1,或者由1变为0)已知某中二元码
称为第k位码元,二元码是通信中常用的码,但在通信过程中有时会发生码元错误(即码元由0变为1,或者由1变为0)已知某中二元码![]() 的码元满足如下校验方程组:
的码元满足如下校验方程组: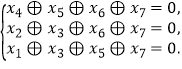 其中运算
其中运算![]() 定义为:
定义为:![]() 现已知一个这种二元码在通信过程中仅在第k位发生码元错误后变成了1101101,那么利用上述校验方程组可判定k等于 。
现已知一个这种二元码在通信过程中仅在第k位发生码元错误后变成了1101101,那么利用上述校验方程组可判定k等于 。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
x |
|
| |||
| 0 | 5 | -5 | 0 |
(Ⅰ)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数![]() 的解析式;
的解析式;
(Ⅱ)将![]() 图象上所有点向左平行移动
图象上所有点向左平行移动![]() 个单位长度,得到
个单位长度,得到![]() 的图象. 若
的图象. 若![]() 图象的一个对称中心为
图象的一个对称中心为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
时间代号t | 1 | 2 | 3 | 4 | 5 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
(1)求y关于t的回归方程![]()
(2)用所求回归方程预测该地区2015年(![]() )的人民币储蓄存款.
)的人民币储蓄存款.
附:回归方程![]() 中
中
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com