
| A、10π | B、9π | C、8π | D、7π |
| 12+22+22 |
| 9 |
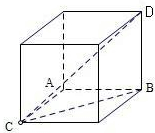 解:∵DB⊥平面ABC,AB⊥AC,且AC=1,DB=AB=2,
解:∵DB⊥平面ABC,AB⊥AC,且AC=1,DB=AB=2,| 12+22+22 |
| 9 |
| 3 |
| 2 |
| 3 |
| 2 |


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:
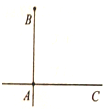 如图,两高速公路线垂直相交于站A,若已知AB=100千米,甲汽车从A站出发,沿AC方向以50千米/小时的速度行驶,同时乙汽车从B站出发,一年BA方向以v千米/小时的速度行驶,至A站即停止前行(甲车仍继续行驶)(两车的车长忽略不计).
如图,两高速公路线垂直相交于站A,若已知AB=100千米,甲汽车从A站出发,沿AC方向以50千米/小时的速度行驶,同时乙汽车从B站出发,一年BA方向以v千米/小时的速度行驶,至A站即停止前行(甲车仍继续行驶)(两车的车长忽略不计).查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| 3 |
10
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68),再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.
某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68),再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.| 组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的比例 |
| 第1组 | [18,28) | 5 | 0.5 |
| 第2组 | [28,38) | 18 | a |
| 第3组 | [38,48) | 27 | 0.9 |
| 第4组 | [48,58) | x | 0.36 |
| 第5组 | [58,68) | 3 | 0.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com