
分析 分别在直角、锐角、钝角三角形中,利用锐角的正弦函数进行证明.
解答 证明: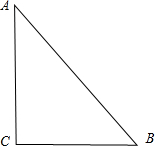 在RT△ABC中,如图所示:
在RT△ABC中,如图所示:
C=90°,设AB=c、BC=a、AC=b,
∴sinA=$\frac{BC}{AB}$=$\frac{a}{c}$,sinB=$\frac{AC}{AB}$=$\frac{b}{c}$,
则c=$\frac{a}{sinA}$,c=$\frac{b}{sinB}$,
又∵sinC=1,c=$\frac{c}{sinC}$,
∴$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$;
在锐角△ABC中,如图所示: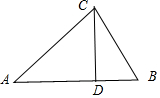
作CD⊥AB,垂足为D,设AB=c、BC=a、AC=b,
∴sinA=$\frac{CD}{AC}$=$\frac{CD}{b}$,sinB=$\frac{CD}{BC}$=$\frac{CD}{a}$,
则CD=bsinA,CD=asinB,
∴bsinA=asinB,则$\frac{a}{sinA}=\frac{b}{sinB}$,
同理可证$\frac{b}{sinB}$=$\frac{c}{sinC}$,
∴$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$在锐角△ABC中成立;
在钝角△ABC中,如图所示:
A为钝角,延长BA、作CD⊥AB,垂足为D,
设AB=c、BC=a、AC=b,
在RT△ACD中,sin∠CAD=sin(π-A)=$\frac{CD}{AC}$=$\frac{CD}{b}$,
则sinA=$\frac{CD}{AC}$=$\frac{CD}{b}$,
在RT△BCD中,sinB=$\frac{CD}{BC}$=$\frac{CD}{a}$,
则CD=bsinA,CD=asinB,
∴bsinA=asinB,则$\frac{a}{sinA}=\frac{b}{sinB}$,
作BC边上的高线可得,$\frac{b}{sinB}$=$\frac{c}{sinC}$,
∴$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$在钝角△ABC中成立;
综上,在任意△ABC中$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$成立.
点评 本题考查正弦定理的证明,以及锐角的正弦函数的应用,考查从特殊到一般的证明方法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $(-3,-\frac{5}{2})$ | B. | $(2,\frac{5}{2})$ | C. | $(\frac{5}{2},3)$ | D. | $(-3,\frac{5}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
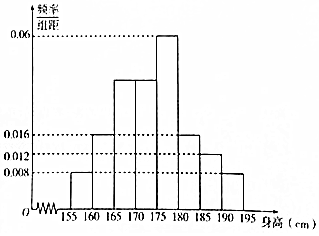 从某校高一年级1000名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米到195厘米之间,将测量结果分为八组:第一组[155,160),第二组[160,165),…,第八组[190,195),得到频率分布直方图如图所示.
从某校高一年级1000名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米到195厘米之间,将测量结果分为八组:第一组[155,160),第二组[160,165),…,第八组[190,195),得到频率分布直方图如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com