
【题目】已知f(x)=lg(x+1)
(1)若0<f(1﹣2x)﹣f(x)<1,求x的取值范围;
(2)若g(x)是以2为周期的偶函数,且当0≤x≤1时,g(x)=f(x),求函数y=g(x)(x∈[1,2])的反函数.
【答案】
(1)解:f(1﹣2x)﹣f(x)=lg(1﹣2x+1)﹣lg(x+1)=lg(2﹣2x)﹣lg(x+1),
要使函数有意义,则
由 ![]() 解得:﹣1<x<1.
解得:﹣1<x<1.
由0<lg(2﹣2x)﹣lg(x+1)=lg ![]() <1得:1<
<1得:1< ![]() <10,
<10,
∵x+1>0,
∴x+1<2﹣2x<10x+10,
∴ ![]() .
.
由 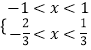 ,得:
,得: ![]() .
.
(2)解:当x∈[1,2]时,2﹣x∈[0,1],
∴y=g(x)=g(x﹣2)=g(2﹣x)=f(2﹣x)=lg(3﹣x),
由单调性可知y∈[0,lg2],
又∵x=3﹣10y,
∴所求反函数是y=3﹣10x,x∈[0,lg2].
【解析】(1)应用对数函数结合对数的运算法则进行求解即可;(2)结合函数的奇偶性和反函数知识进行求解.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
【题目】智能手机的出现,改变了我们的生活,同时也占用了我们大量的学习时间.某市教育机构从![]() 名手机使用者中随机抽取
名手机使用者中随机抽取![]() 名,得到每天使用手机时间(单位:分钟)的频率分布直方图(如图所示),其分组是:
名,得到每天使用手机时间(单位:分钟)的频率分布直方图(如图所示),其分组是: ![]() ,
,![]() .
.

(1)根据频率分布直方图,估计这![]() 名手机使用者中使用时间的中位数是多少分钟? (精确到整数)
名手机使用者中使用时间的中位数是多少分钟? (精确到整数)
(2)估计手机使用者平均每天使用手机多少分钟? (同一组中的数据以这组数据所在区间中点的值作代表)
(3)在抽取的![]() 名手机使用者中在
名手机使用者中在![]() 和
和![]() 中按比例分别抽取
中按比例分别抽取![]() 人和
人和![]() 人组成研究小组,然后再从研究小组中选出
人组成研究小组,然后再从研究小组中选出![]() 名组长.求这
名组长.求这![]() 名组长分别选自
名组长分别选自![]() 和
和![]() 的概率是多少?
的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种农作物可以生长在滩涂和盐碱地,它的灌溉是将海水稀释后进行灌溉.某实验基地为了研究海水浓度![]() 对亩产量
对亩产量![]() (吨)的影响,通过在试验田的种植实验,测得了该农作物的亩产量与海水浓度的数据如下表:
(吨)的影响,通过在试验田的种植实验,测得了该农作物的亩产量与海水浓度的数据如下表:
海水浓度 |
|
|
|
|
|
亩产量 |
|
|
|
|
|
残差 |
|
|
|
|
|
绘制散点图发现,可以用线性回归模型拟合亩产量![]() (吨)与海水浓度
(吨)与海水浓度![]() 之间的相关关系,用最小二乘法计算得
之间的相关关系,用最小二乘法计算得![]() 与
与![]() 之间的线性回归方程为
之间的线性回归方程为![]() .
.
(1)求![]() 的值;
的值;
(2)统计学中常用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越大,回归效果越好,如假设
越大,回归效果越好,如假设![]() ,就说明预报变量
,就说明预报变量![]() 的差异有
的差异有![]() 是解释变量
是解释变量![]() 引起的.请计算相关指数
引起的.请计算相关指数![]() (精确到
(精确到![]() ),并指出亩产量的变化多大程度上是由浇灌海水浓度引起的?
),并指出亩产量的变化多大程度上是由浇灌海水浓度引起的?
(附:残差![]() ,相关指数
,相关指数 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且a2an=S2+Sn对一切正整数n都成立.
(1)求a1 , a2的值;
(2)设a1>0,数列{lg ![]() }的前n项和为Tn , 当n为何值时,Tn最大?并求出Tn的最大值.
}的前n项和为Tn , 当n为何值时,Tn最大?并求出Tn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设an= ![]() sin
sin ![]() ,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正数的个数是( )
,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正数的个数是( )
A.25
B.50
C.75
D.100
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数集X={﹣1,x1 , x2 , …,xn},其中0<x1<x2<…<xn , n≥2,定义向量集Y={ ![]() =(s,t),s∈X,t∈X},若对任意
=(s,t),s∈X,t∈X},若对任意 ![]() ,存在
,存在 ![]() ,使得
,使得 ![]() ,则称X具有性质P.例如{﹣1,1,2}具有性质P.
,则称X具有性质P.例如{﹣1,1,2}具有性质P.
(1)若x>2,且{﹣1,1,2,x}具有性质P,求x的值;
(2)若X具有性质P,求证:1∈X,且当xn>1时,x1=1;
(3)若X具有性质P,且x1=1、x2=q(q为常数),求有穷数列x1 , x2 , …,xn的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着共享单车的蓬勃发展,越来越多的人将共享单车作为短距离出行的交通工具.为了解不同年龄的人们骑乘单车的情况,某共享单车公司对某区域不同年龄的骑乘者进行了调查,得到数据如下:
年龄 | 15 | 25 | 35 | 45 | 55 | 65 |
骑乘人数 | 95 | 80 | 65 | 40 | 35 | 15 |
(1)求![]() 关于
关于![]() 的线性回归方程,并估计年龄为40岁人群的骑乘人数;
的线性回归方程,并估计年龄为40岁人群的骑乘人数;
(2)为了回馈广大骑乘者,该公司在五一当天通过![]() 向每位骑乘者的前两次骑乘分别随机派送一张面额为1元,或2元,或3元的骑行券.已知骑行一次获得1元券,2元券,3元券的概率分别是
向每位骑乘者的前两次骑乘分别随机派送一张面额为1元,或2元,或3元的骑行券.已知骑行一次获得1元券,2元券,3元券的概率分别是![]() ,
,![]() ,
,![]() ,且每次获得骑行券的面额相互独立.若一名骑乘者五一当天使用了两次该公司的共享单车,记该骑乘者当天获得的骑行券面额之和为
,且每次获得骑行券的面额相互独立.若一名骑乘者五一当天使用了两次该公司的共享单车,记该骑乘者当天获得的骑行券面额之和为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:
 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生产企业研发了一种新产品,该产品在试销一个阶段后得到销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:万件)之间的一组数据,如下表所示:
(单位:万件)之间的一组数据,如下表所示:
销售单价 |
|
|
|
|
|
销售量 |
|
|
|
|
|
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)从反馈的信息来看,消费者对该产品的心理价(单位:元/件)在![]() 内,已知该产品的成本是
内,已知该产品的成本是![]() 元,那么在消费者对该产品的心理价的范围内,销售单价定为多少时,企业才能获得最大利润?(注:利润=销售收入-成本)
元,那么在消费者对该产品的心理价的范围内,销售单价定为多少时,企业才能获得最大利润?(注:利润=销售收入-成本)
参考数据:![]()
参考公式: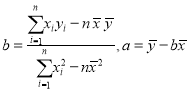
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com