
分析 (Ⅰ)由f(1)=f(3)=-1求出b,c值,得到函数f(x)的解析式,进而可得函数g(x)的解析式,由函数g(x)有两个零点x1,x2,且x1<4<x2,可得g(4)<0,解得实数a的取值范围;
(Ⅱ)根据已知中“陡峭函数”的定义,结合二次函数的图象和性质,分类讨论,可得满足条件的实数a的取值范围.
解答 (本小题满分12分)
解:(Ⅰ)由$\left\{\begin{array}{l}f(1)=-1\\ f(3)=-1\end{array}\right.⇒\left\{\begin{array}{l}1+2b+c=-1\\ 9+6b+c=-1\end{array}\right.⇒\left\{\begin{array}{l}b=-2\\ c=2\end{array}\right.$,
即f(x)=x2-4x+2,…(1分)
由题设可知g(x)=(x-a)2-4(x-a)+2-a2=x2-(2a+4)x+4a+2,…(2分)
因为g(x)有两个零点x1,x2,且x1<4<x2,
∴g(4)=16-4(2a+4)+4a+2<0,$⇒a>\frac{1}{2}$,
又a>0,于是实数a的取值范围为$({\frac{1}{2},+∞})$.…(5分)
(Ⅱ)由g(x)=x2-(2a+4)x+4a+2可知,其对称轴为x=a+2,…(6分)
①当0<a≤2时,a+2≥2a,函数g(x)在区间[a,2a]上单调递减,
最小值λ=g(2a)=-4a+2,最大值μ=g(a)=-a2+2,
则$\frac{μ-λ}{2a-a}>8⇒\frac{{4a-{a^2}}}{a}>8⇒\left\{\begin{array}{l}4-a>8\\ 0<a≤2\end{array}\right.$,显然此时a不存在,…(8分)
②当2<a≤4时,a<a+2<2a,最小值λ=g(a+2)=-a2-2,
又$a+2≥\frac{3a}{2}$,最大值μ=g(a)=-a2+2,则$\frac{μ-λ}{2a-a}>8⇒\frac{4}{a}>8$,$⇒0<a<\frac{1}{2}$,又2<a≤4,此时a亦不存在,…(10分)
③当a>4时,a<a+2<2a,最小值λ=g(a+2)=-a2-2,
又$a+2<\frac{3a}{2}$,故最大值μ=g(2a)=-4a+2,
则$\frac{μ-λ}{2a-a}>8⇒\frac{{{a^2}-4a+4}}{a}>8⇒\left\{\begin{array}{l}{a^2}-12a+4>0\\ a>4\end{array}\right.$,$⇒\left\{\begin{array}{l}a<6-4\sqrt{2},或a>6+4\sqrt{2}\\ a>4\end{array}\right.$,即$a>6+4\sqrt{2}$,
综上可知,实数a的取值范围为$({6+4\sqrt{2},+∞})$.…(12分)
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
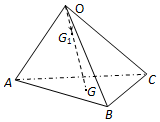
| A. | $\overrightarrow{O{G}_{1}}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$ | B. | $\overrightarrow{O{G}_{1}}$=$\frac{1}{3}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$ | ||
| C. | $\overrightarrow{O{G}_{1}}$=$\frac{3}{4}$$\overrightarrow{OA}$+$\frac{3}{4}$$\overrightarrow{OB}$+$\frac{3}{4}$$\overrightarrow{OC}$ | D. | $\overrightarrow{O{G}_{1}}$=$\frac{1}{9}$$\overrightarrow{OA}$+$\frac{1}{9}$$\overrightarrow{OB}$+$\frac{1}{9}$$\overrightarrow{OC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{25}$ | B. | $\frac{4}{5}$ | C. | $\frac{9}{16}$ | D. | $\frac{9}{20}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
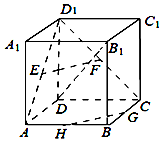 如图,已知正方体ABCD-A1B1C1D1,E,F,G,H分别是AD1、CD1、BC、AB的中点.
如图,已知正方体ABCD-A1B1C1D1,E,F,G,H分别是AD1、CD1、BC、AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com