
ЁОЬтФПЁП2018Фъ2дТ9-25ШеЃЌЕк23НьЖЌАТЛсдкКЋЙњЦНВ§Ойаа.4ФъКѓЃЌЕк24 НьЖЌАТЛсНЋдкжаЙњББОЉКЭеХМвПкОйаа.ЮЊСЫаћДЋЖЌАТЛсЃЌФГДѓбЇдкЦНВ§ЖЌАТЛсПЊФЛКѓЕФЕкЖўЬьЃЌДгШЋаЃбЇЩњжаЫцЛњГщШЁСЫ120УћбЇЩњЃЌЖдЪЧЗёЪеПДЦНВ§ЖЌАТЛсПЊФЛЪНЧщПіНјааСЫЮЪОэЕїВщЃЌЭГМЦЪ§ОнШчЯТЃК

ЃЈ1ЃЉИљОнЩЯБэЫЕУїЃЌФмЗёга![]() ЕФАбЮеШЯЮЊЃЌЪеПДПЊФЛЪНгыадБ№гаЙиЃП
ЕФАбЮеШЯЮЊЃЌЪеПДПЊФЛЪНгыадБ№гаЙиЃП
ЃЈ2ЃЉЯжДгВЮгыЮЪОэЕїВщЧвЪеПДСЫПЊФЛЪНЕФбЇЩњжаЃЌВЩгУАДадБ№ЗжВуГщбљЕФЗНЗЈЃЌбЁШЁ12ШЫВЮМг2022ФъББОЉЖЌАТЛсжОдИепаћДЋЛюЖЏ.ШєДгет12ШЫжаЫцЛњбЁШЁ3ШЫЕНаЃЙуВЅеОПЊеЙЖЌАТЛсМАБљбЉЯюФПЕФаћДЋНщЩмЃЌЩшбЁШЁЕФ3 ШЫжаХЎЩњШЫЪ§ЮЊ![]() ЃЌаДГі
ЃЌаДГі![]() ЕФЗжВМСаЃЌВЂЧѓ
ЕФЗжВМСаЃЌВЂЧѓ![]() .
.
ИНЃК![]() ЃЌЦфжа
ЃЌЦфжа![]() .
.

ЁОД№АИЁПЃЈ1ЃЉгаЃЈ2ЃЉМћНтЮі
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉжБНгДњШыЙЋЪНМДПЩЃЛ
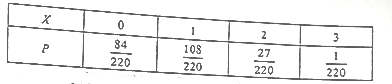
ЃЈ2ЃЉИљОнЗжВуГщбљЗНЗЈЃЌбЁШЁЕФ12ШЫжаЃЌФаЩњга9ШЫЃЌХЎЩњга3ШЫЃЛЬтвтПЩжЊЃЌ![]() ЕФПЩФмШЁжЕга0, 1, 2, 3.ЃЌЗжБ№ЧѓГіЦфИХТЪМДПЩ.
ЕФПЩФмШЁжЕга0, 1, 2, 3.ЃЌЗжБ№ЧѓГіЦфИХТЪМДПЩ.
ЯъНтЃКЃЈ1ЃЉвђЮЊ![]() ЃЌ
ЃЌ
Ыљвдга![]() ЕФАбЮеШЯЮЊЃЌЪеПДПЊФЛЪНгыадБ№гаЙи.
ЕФАбЮеШЯЮЊЃЌЪеПДПЊФЛЪНгыадБ№гаЙи.
ЃЈ2ЃЉИљОнЗжВуГщбљЗНЗЈЕУЃЌФаЩњ![]() ШЫЃЌХЎЩњ
ШЫЃЌХЎЩњ![]() ШЫ
ШЫ
ЫљвдбЁШЁЕФ12ШЫжаЃЌФаЩњга9ШЫЃЌХЎЩњга3ШЫ.
гЩЬтвтПЩжЊЃЌ![]() ЕФПЩФмШЁжЕга0, 1, 2, 3.
ЕФПЩФмШЁжЕга0, 1, 2, 3.
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЕФЗжВМСаЪЧЃК
ЕФЗжВМСаЪЧЃК
Ёр![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшбљБОЪ§Онx1 ЃЌ x2 ЃЌ ЁЃЌx10ЕФОљжЕКЭЗНВюЗжБ№ЮЊ1КЭ4ЃЌШєyi=xi+aЃЈaЮЊЗЧСуГЃЪ§ЃЌi=1ЃЌ2ЃЌЁЃЌ10ЃЉЃЌдђy1 ЃЌ y2 ЃЌ ЁЃЌy10ЕФОљжЕКЭЗНВюЗжБ№ЮЊЃЈ ЃЉ
A.1+aЃЌ4
B.1+aЃЌ4+a
C.1ЃЌ4
D.1ЃЌ4+a
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдкШёНЧ![]() жаЃЌНЧ
жаЃЌНЧ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЫљЖдЕФБпЗжБ№ЮЊ
ЫљЖдЕФБпЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]()
ЃЈ1ЃЉЧѓНЧ![]() ДѓаЁЃЛ
ДѓаЁЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЁЃ
ЕФШЁжЕЗЖЮЇЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛКажазАга9еХИїаДгавЛИіЪ§зжЕФПЈЦЌЃЌЦфжа4еХПЈЦЌЩЯЕФЪ§зжЪЧ1,3еХПЈЦЌЩЯЕФЪ§зжЪЧ2,2еХПЈЦЌЩЯЕФЪ§зжЪЧ3ЃЌДгКажаШЮШЁ3еХПЈЦЌ.
ЃЈ1ЃЉЧѓЫљШЁ3еХПЈЦЌЩЯЕФЪ§зжЭъШЋЯрЭЌЕФИХТЪ;
ЃЈ2ЃЉ![]() БэЪОЫљШЁ3еХПЈЦЌЩЯЕФЪ§зжЕФжаЮЛЪ§ЃЌЧѓ
БэЪОЫљШЁ3еХПЈЦЌЩЯЕФЪ§зжЕФжаЮЛЪ§ЃЌЧѓ![]() ЕФЗжВМСагыЪ§бЇЦкЭћ.
ЕФЗжВМСагыЪ§бЇЦкЭћ.
ЃЈзЂЃКШєШ§ИіЪ§![]() Тњзу
Тњзу![]() ЃЌдђГЦ
ЃЌдђГЦ![]() ЮЊетШ§ИіЪ§ЕФжаЮЛЪ§ЃЉ.
ЮЊетШ§ИіЪ§ЕФжаЮЛЪ§ЃЉ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЕФЖЈвхгђЮЊ
ЕФЖЈвхгђЮЊ![]() ЃЌВПЗжЖдгІжЕШчЯТБэЃЌ
ЃЌВПЗжЖдгІжЕШчЯТБэЃЌ![]() ЕФЕМКЏЪ§
ЕФЕМКЏЪ§![]() ЕФЭМЯѓШчЭМЫљЪОЃЌИјГіЙигк
ЕФЭМЯѓШчЭМЫљЪОЃЌИјГіЙигк![]() ЕФЯТСаУќЬтЃК
ЕФЯТСаУќЬтЃК
ЂйКЏЪ§![]() дк
дк![]() ДІШЁЕУМЋаЁжЕ;
ДІШЁЕУМЋаЁжЕ;
ЂкКЏЪ§![]() дк
дк![]() ЪЧМѕКЏЪ§ЃЌдк
ЪЧМѕКЏЪ§ЃЌдк![]() ЪЧдіКЏЪ§ЃЛ
ЪЧдіКЏЪ§ЃЛ
ЂлЕБ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() га4ИіСуЕуЃЛ
га4ИіСуЕуЃЛ
ЂмШчЙћЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФзюДѓжЕЪЧ2ЃЌФЧУД
ЕФзюДѓжЕЪЧ2ЃЌФЧУД![]() ЕФзюаЁжЕЮЊ0.
ЕФзюаЁжЕЮЊ0.
ЦфжаЫљгаЕФе§ШЗУќЬтЪЧ__________(аДГіе§ШЗУќЬтЕФађКХ).

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§
fЃЈxЃЉ=ЃЈcosxЉxЃЉЃЈІа+2xЃЉЉ ![]() ЃЈsinx+1ЃЉ
ЃЈsinx+1ЃЉ
gЃЈxЃЉ=3ЃЈxЉІаЃЉcosxЉ4ЃЈ1+sinxЃЉlnЃЈ3Љ ![]() ЃЉ
ЃЉ
жЄУїЃК
ЃЈ1ЃЉДцдкЮЈвЛx0ЁЪЃЈ0ЃЌ ![]() ЃЉЃЌЪЙfЃЈx0ЃЉ=0ЃЛ
ЃЉЃЌЪЙfЃЈx0ЃЉ=0ЃЛ
ЃЈ2ЃЉДцдкЮЈвЛx1ЁЪЃЈ ![]() ЃЌІаЃЉЃЌЪЙgЃЈx1ЃЉ=0ЃЌЧвЖдЃЈЂёЃЉжаЕФx0 ЃЌ гаx0+x1ЃМІаЃЎ
ЃЌІаЃЉЃЌЪЙgЃЈx1ЃЉ=0ЃЌЧвЖдЃЈЂёЃЉжаЕФx0 ЃЌ гаx0+x1ЃМІаЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈЬтЮФЃЉвбжЊКЏЪ§![]()
ЃЈIЃЉЕБ![]() ЪБЃЌЧѓКЏЪ§
ЪБЃЌЧѓКЏЪ§![]() ЕФЕЅЕїЧјМфЃЛ
ЕФЕЅЕїЧјМфЃЛ
ЃЈIIЃЉЕБ![]() ЪБЃЌШєЖдгкЧјМф
ЪБЃЌШєЖдгкЧјМф![]() ЩЯЕФШЮвтСНИіВЛЯрЕШЕФЪЕЪ§
ЩЯЕФШЮвтСНИіВЛЯрЕШЕФЪЕЪ§![]() ЃЌЖМга
ЃЌЖМга![]() ГЩСЂЃЌЧѓЪЕЪ§
ГЩСЂЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцЛњНЋ1ЃЌ2ЃЌЁЃЌ2nЃЈnЁЪN* ЃЌ nЁн2ЃЉет2nИіСЌаје§ећЪ§ЗжГЩAЁЂBСНзщЃЌУПзщnИіЪ§ЃЌAзщзюаЁЪ§ЮЊa1 ЃЌ зюДѓЪ§ЮЊa2ЃЛBзщзюаЁЪ§ЮЊb1 ЃЌ зюДѓЪ§ЮЊb2ЃЛМЧІЮ=a2Љa1 ЃЌ ІЧ=b2Љb1 ЃЎ
ЃЈ1ЃЉЕБn=3ЪБЃЌЧѓІЮЕФЗжВМСаКЭЪ§бЇЦкЭћЃЛ
ЃЈ2ЃЉCБэЪОЪТМўЁАІЮгыІЧЕФШЁжЕЧЁКУЯрЕШЁБЃЌЧѓЪТМўCЗЂЩњЕФИХТЪPЃЈCЃЉЃЛ
ЃЈ3ЃЉЖдЃЈ2ЃЉжаЕФЪТМўCЃЌ ![]() БэЪОCЕФЖдСЂЪТМўЃЌХаЖЯPЃЈCЃЉКЭPЃЈ
БэЪОCЕФЖдСЂЪТМўЃЌХаЖЯPЃЈCЃЉКЭPЃЈ ![]() ЃЉЕФДѓаЁЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЃЉЕФДѓаЁЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са{an}Тњзуa1=1ЃЌ|an+1Љan|=pn ЃЌ nЁЪN* ЃЎ
ЃЈ1ЃЉШє{an}ЪЧЕндіЪ§СаЃЌЧвa1 ЃЌ 2a2 ЃЌ 3a3ГЩЕШВюЪ§СаЃЌЧѓpЕФжЕЃЛ
ЃЈ2ЃЉШєp= ![]() ЃЌЧв{a2nЉ1}ЪЧЕндіЪ§СаЃЌ{a2n}ЪЧЕнМѕЪ§СаЃЌЧѓЪ§Са{an}ЕФЭЈЯюЙЋЪНЃЎ
ЃЌЧв{a2nЉ1}ЪЧЕндіЪ§СаЃЌ{a2n}ЪЧЕнМѕЪ§СаЃЌЧѓЪ§Са{an}ЕФЭЈЯюЙЋЪНЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com