
分析 (1)利用$M(\sqrt{3},\frac{{\sqrt{10}}}{2})$,$N(2,\frac{{\sqrt{15}}}{3})$两点在椭圆C上,列出方程组求解a,b即可得到椭圆方程.
(2)通过当直线l的斜率不存在时,计算结果,当直线l的斜率存在,设其方程为y=k(x-1),联立直线与椭圆方程,设A(x1,y1),B(x2,y2),利用韦达定理表示向量关系式,然后求解k的范围即可.
解答 解:(1)由$M(\sqrt{3},\frac{{\sqrt{10}}}{2})$,$N(2,\frac{{\sqrt{15}}}{3})$两点在椭圆C上,得$\left\{{\begin{array}{l}{\frac{3}{a^2}+\frac{5}{{2{b^2}}}=1}\\{\frac{4}{a^2}+\frac{5}{{3{b^2}}}=1}\end{array}}\right.$…(2分)
解得a2=6,b2=5,故椭圆C的方程为$\frac{x^2}{6}+\frac{y^2}{5}=1$. …(5分)
(2)由(1)知F(1,0),
当直线l的斜率不存在时,计算得${k_{DA}}×{k_{DB}}=-\frac{25}{24}$. …(6分)
当直线l的斜率存在,设其方程为y=k(x-1)
由$\left\{{\begin{array}{l}{y=k(x-1)}\\{5{x^2}+6{y^2}=3}\end{array}}\right.⇒(6{k^2}+5){x^2}-12{k^2}x+6{k^2}-30=0$①…(7分)
设A(x1,y1),B(x2,y2),则由①得$\left\{{\begin{array}{l}{{x_1}+{x_2}=\frac{{12{k^2}}}{{6{k^2}+5}}}\\{{x_1}+{x_2}=\frac{{6{k^2}-30}}{{6{k^2}+5}}}\end{array}}\right.$②…(8分)
故${k_{DA}}×{k_{DB}}=\frac{y_1}{{{x_1}-3}}×\frac{y_2}{{{x_2}-3}}=\frac{{k({x_1}-1)k({x_2}-1)}}{{({x_1}-3)({x_2}-3)}}={k^2}\frac{{{x_1}{x_2}-({x_1}+{x_2})+1}}{{{x_1}{x_2}-3({x_1}+{x_2})+9}}$③…(9分)
将②代入③化简得${k_{DA}}×{k_{DB}}={k^2}\frac{{{x_1}{x_2}-({x_1}+{x_2})+1}}{{{x_1}{x_2}-3({x_1}+{x_2})+9}}=\frac{{-25{k^2}}}{{24{k^2}+15}}$…(10分)
当k=0时,得kDA×kDB=0,当k≠0时,${k_{DA}}×{k_{DB}}=-\frac{25}{{24+\frac{15}{k^2}}}$知$-\frac{25}{24}<{k_{DA}}×{k_{DB}}<0$,
综上可知,$-\frac{25}{24}≤{k_{DA}}×{k_{DB}}≤0$
即直线DA、DB的斜率之积的取值范围是$[-\frac{25}{24},0]$…(12分)
点评 本题考查椭圆的方程的求法,椭圆的简单性质,直线与椭圆的位置关系的综合应用,考查设而不求,转化思想的应用.


科目:高中数学 来源: 题型:选择题
| A. | a≥9 | B. | a≤9 | C. | a≤8 | D. | a≥8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$i | C. | -$\frac{2\sqrt{5}}{5}$ | D. | -$\frac{2\sqrt{5}}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪(2,+∞) | B. | [-2,2] | C. | (-∞,-4)∪(4,+∞) | D. | [-4,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
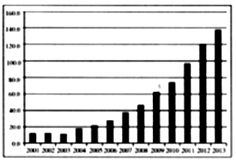 2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )
2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )| A. | y=ax2+bx+c | B. | y=aex+b | C. | y=aax+b | D. | y=alnx+b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
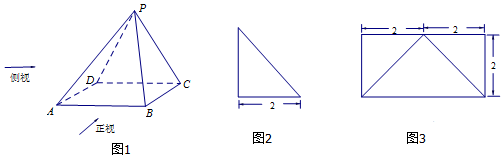
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com