
【题目】如图,直三棱柱ABC—A1B1C1中,∠ACB=90°,AC=AA1=1,![]() , AB1与A1B相交于点D,M为B1C1的中点 .
, AB1与A1B相交于点D,M为B1C1的中点 .

(1)求证:CD⊥平面BDM;
(2)求平面B1BD与平面CBD所成锐二面角的余弦值.
【答案】(1)见解析 (2) ![]()
【解析】
(1)先以CB为x轴,CC1为y轴,CA为z轴建立空间直角坐标系,然后分别确定点B、M、D的坐标,利用向量法证明CD⊥平面BDM.(2)求出平面BDC的法向量和平面B1BD的法向量,利用向量法能求出平面B1BD与平面CBD所成锐二面角余弦值.
证明:(1)由题意知AC、BC、CC1两两垂直,
则以CB为x轴,CC1为y轴,CA为z轴建立空间直角坐标系.
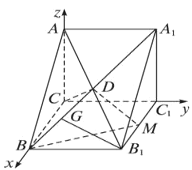
∵CB![]() ,CC1=AA1=1,CA=1,M为B1C1的中点.
,CC1=AA1=1,CA=1,M为B1C1的中点.
∴B(![]() ,0,0),M(
,0,0),M(![]() ,1,0),
,1,0),
又∵点D是矩形AA1B1B的两条对角线的交点,
∴D(![]() ,
,![]() ,
,![]() ),
),
则![]() (
(![]() ),
),![]() (
(![]() ,1,0),
,1,0),![]() (
(![]() ,
,![]() ),
),
∴![]()
![]() ,
,![]() 0,
0,
∴CD⊥BM,CD⊥BD,
又BM∩BD=B,∴CD⊥平面BDM.
(2)由(1)
![]() (
(![]() ),
),![]() (
(![]() ),
),
设平面BDC的法向量![]() (x,y,z),
(x,y,z),
则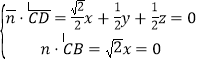 ,取y=1,得
,取y=1,得![]() (0,1,﹣1),
(0,1,﹣1),
B1(![]() ,1,0),
,1,0),![]() (
(![]() ,
,![]() ),
),![]() (0,1,0),
(0,1,0),
设平面B1BD的法向量![]() (a,b,c),
(a,b,c),
则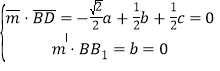 ,取a=1,得
,取a=1,得![]() (1,0,
(1,0,![]() ),
),
设平面B1BD与平面CBD所成锐二面角为θ,
则cosθ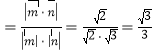 .
.
∴平面B1BD与平面CBD所成锐二面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某校参加夏令营的同学有3名男同学![]() 和3名女同学
和3名女同学![]() ,其所属年级情况如下表:
,其所属年级情况如下表:
高一年级 | 高二年级 | 高三三年级 | |
男同学 |
|
|
|
女同学 |
|
|
|
现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同)
(1)用表中字母写出这个试验的样本空间;
(2)设![]() 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,写出事件
为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,写出事件![]() 的样本点,并求事件
的样本点,并求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司有![]() 四辆汽车,其中
四辆汽车,其中![]() 车的车牌尾号为0,
车的车牌尾号为0,![]() 两辆车的车牌尾号为6,
两辆车的车牌尾号为6,![]() 车的车牌尾号为5,已知在非限行日,每辆车都有可能出车或不出车.已知
车的车牌尾号为5,已知在非限行日,每辆车都有可能出车或不出车.已知![]() 两辆汽车每天出车的概率为
两辆汽车每天出车的概率为![]() ,
,![]() 两辆汽车每天出车的概率为
两辆汽车每天出车的概率为![]() ,且四辆汽车是否出车是相互独立的.
,且四辆汽车是否出车是相互独立的.
该公司所在地区汽车限行规定如下:

(1)求该公司在星期四至少有2辆汽车出车的概率;
(2)设![]() 表示该公司在星期一和星期二两天出车的车辆数之和,求
表示该公司在星期一和星期二两天出车的车辆数之和,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机的普及,网络搜题软件走进了生活,有教育工作者认为,网搜答案可以起到帮助人们学习的作用,但对多数学生来讲,过度网搜答案容易养成依赖心理,对学习能力造成损害.为了了解学生网搜答案的情况,某学校对学生一月内进行网搜答案的次数进行了问卷调查,并从参与调查的学生中抽取了男、女生各100人进行抽样分析,制成如下频率分布直方图:

记事件“男生1月内网搜答案次数不高于30次”为![]() ,根据频率分布直方图得到
,根据频率分布直方图得到![]() 的估计值为0.65
的估计值为0.65
(1)求![]() 的值;
的值;
(2)若一学生在1月内网搜答案次数超过50次,则称该学生为“依赖型”,现从样本内的“依赖型”学生中,抽取3人谈话,求抽取的女生人数X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时.某地上班族![]() 中的成员仅以自驾或公交方式通勤.分析显示:当
中的成员仅以自驾或公交方式通勤.分析显示:当![]() 中
中![]() (
(![]() )的成员自驾时,自驾群体的人均通勤时间为
)的成员自驾时,自驾群体的人均通勤时间为 (单位:分钟),而公交群体的人均通勤时间不受
(单位:分钟),而公交群体的人均通勤时间不受![]() 影响,恒为
影响,恒为![]() 分钟,试根据上述分析结果回答下列问题:
分钟,试根据上述分析结果回答下列问题:
(1)当![]() 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
(2)求该地上班族![]() 的人均通勤时间
的人均通勤时间![]() 的表达式;讨论
的表达式;讨论![]() 的单调性,并说明其实际意义.
的单调性,并说明其实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心为![]() 的圆过原点
的圆过原点![]() ,且直线
,且直线![]() 与圆
与圆![]() 相切于点
相切于点![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)已知过点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,且直线
,且直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点.
两点.
①若![]() ,求弦
,求弦![]() 的长;
的长;
②若圆![]() 上存在点
上存在点![]() ,使得
,使得![]() 成立,求直线
成立,求直线![]() 的斜率
的斜率![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com