
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
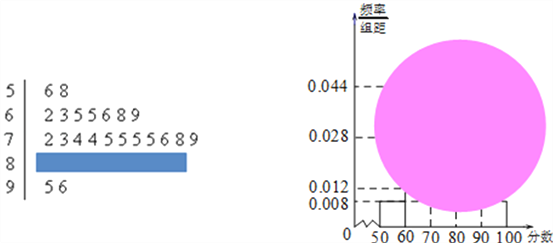
(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间矩形的高;
(Ⅲ)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在[90,100)之间的概率.
【答案】(1)25,(2)0.012,(3)0.7.
【解析】 试题分析:(Ⅰ)先由频率分布直方图求出[50,60)的频率,结合茎叶图中得分在[50,60)的人数即可求得本次考试的总人数;(Ⅱ)根据茎叶图的数据,利用(Ⅰ)中的总人数减去[50,80)外的人数,即可得到[50,80)内的人数,从而可计算频率分布直方图中[80,90)间矩形的高;(Ⅲ)用列举法列举出所有的基本事件,找出符合题意得基本事件个数,利用古典概型概率计算公式即可求出结果.
(Ⅰ)分数在[50,60)的频率为0.008×10=0.08,
由茎叶图知:分数在[50,60)之间的频数为2,
∴全班人数为![]() .
.
(Ⅱ)分数在[80,90)之间的频数为25﹣22=3;
频率分布直方图中[80,90)间的矩形的高为![]() .
.
(Ⅲ)将[80,90)之间的3个分数编号为a1,a2,a3,[90,100)之间的2个分数编号为b1,b2,
在[80,100)之间的试卷中任取两份的基本事件为:
(a1,a2),(a1,a3),(a1,b1),(a1,b2),(a2,a3),(a2,b1),(a2,b2),(a3,b1),(a3,b2),(b1,b2)共10个,
其中,至少有一个在[90,100)之间的基本事件有7个,
故至少有一份分数在[90,100)之间的概率是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°. 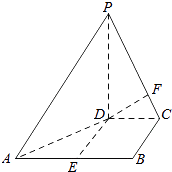
(1)求证:PC⊥BC;
(2)求点A到平面PBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PD垂直于底面ABCD,AD=PD,E分别为AP的中点.
(Ⅰ)求证:DE垂直于平面PAB;
(Ⅱ)设BC =![]() ,AB=2,求直线EB与平面ABD所成的角的大小.
,AB=2,求直线EB与平面ABD所成的角的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为函数f(x)的不动点.已知f(x)=x2+bx+c
(1)若f(x)有两个不动点为﹣3,2,求函数y=f(x)的零点?
(2)若c= ![]() 时,函数f(x)没有不动点,求实数b的取值范围?
时,函数f(x)没有不动点,求实数b的取值范围?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列四个命题:
①函数f(x)= ![]() x﹣lnx(x>0),则y=f(x)在区间(
x﹣lnx(x>0),则y=f(x)在区间( ![]() ,1)内无零点,在区间(1,e)内有零点;
,1)内无零点,在区间(1,e)内有零点;
②函数f(x)=log2(x+ ![]() ),g(x)=1+
),g(x)=1+ ![]() 不都是奇函数;
不都是奇函数;
③若函数f(x)满足f(x﹣1)=﹣f(x+1),且f(1)=2,则f(7)=﹣2;
④设x1、x2是关于x的方程|logax|=k(a>0且a≠1)的两根,则x1x2=1,
其中正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查:生产某产品需投入年固定成本为3万元,每生产x万件,需另投入流动成本为W(x)万元,在年产量不足8万件时,W(x)= ![]() x2+x(万元),在年产量不小于8万件时,W(x)=6x+
x2+x(万元),在年产量不小于8万件时,W(x)=6x+ ![]() ﹣38(万元).通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
﹣38(万元).通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(1)写出年利润L(x)(万元)关于年产量x(万件)的函数解析式;
(2)写出当产量为多少时利润最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司今年一月份推出新产品A,其成本价为492元/件,经试销调查,销售量与销售价的关系如下表:
销售价(x/元件) | 650 | 662 | 720 | 800 |
销售量(y件) | 350 | 333 | 281 | 200 |
由此可知,销售量y(件)与销售价x(元/件)可近似看作一次函数y=kx+b的关系(通常取表中相距较远的两组数据所得一次函数较为精确).
(1)写出以x为自变量的函数y的解析式及定义域;
(2)试问:销售价定为多少时,一月份销售利润最大?并求最大销售利润和此时的销售量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com