
【题目】已知![]() 的外接圆半径
的外接圆半径![]() ,角A、B、C的对边分别是a、b、c,且
,角A、B、C的对边分别是a、b、c,且![]() .
.
(I)求角B和边长b;
(II)求![]() 面积的最大值及取得最大值时的a、c的值,并判断此时三角形的形状.
面积的最大值及取得最大值时的a、c的值,并判断此时三角形的形状.
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
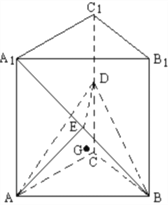
【题目】如图,在直三棱柱![]() 中,底面是等腰直角三角形,
中,底面是等腰直角三角形, ![]() ,侧棱
,侧棱![]() ,D、E分别是
,D、E分别是![]() 与
与![]() 的中点,点E在平面ABD上的射影是
的中点,点E在平面ABD上的射影是![]() 的重心
的重心![]()
(Ⅰ)求![]() 与平面ABD所成角的余弦值
与平面ABD所成角的余弦值
(Ⅱ)求点![]() 到平面
到平面![]() 的距离
的距离
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)的定义域为[0,4],则函数g(x)=f(x)+f(x2)的定义域为( )
A.[0,2]
B.[0,16]
C.[﹣2,2]
D.[﹣2,0]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,其中a>0,且函数f(x)的最大值是
,其中a>0,且函数f(x)的最大值是 ![]()
(1)求实数a的值;
(2)若函数g(x)=lnf(x)﹣b有两个零点,求实数b的取值范围;
(3)若对任意的x∈(0,2),都有f(x)< ![]() 成立,求实数k的取值范围.
成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一列火车从重庆驶往北京,沿途有n个车站(包括起点站重庆和终点站北京).车上有一邮政车厢,每停靠一站便要卸下火车已经过的各站发往该站的邮袋各1个,同时又要装上该站发往以后各站的邮袋各1个,设从第k站出发时,邮政车厢内共有邮袋ak个(k=1,2,…,n).
(1)求数列{ak}的通项公式;
(2)当k为何值时,ak的值最大,求出ak的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点A(0,1),B(0,﹣1),C(1,0),动点P满足: ![]() ,
,
(1)求动点P的轨迹方程,并说明方程表示的曲线类型;
(2)当k=2,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com