设有关于x的一元二次方程x2+2ax+b2=0.
(1)将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为a,第二次出现的点数为b.求上述方程有实根的概率;
(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
解:记事件A=“方程x
2+2ax+b
2=0有实根”.
由△=(2a)
2-4b
2≥0,得:a
2≥b
2所以,当a≥0,b≥0时,方程x
2+2ax+b
2=0有实根?a≥b(2分)
(1)基本事件共6×6=36个,
其中事件A包含21个基本事件:
(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),(4,1),
(4,2),(4,3),(4,4)(5,1),(5,2),(5,3),(5,4),
(5,5),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)
所以

(6分)
(2)全部结果所构成的区域为{(a,b)|0≤a≤3,0≤b≤2},
其面积为S=3×2=6.
又构成事件A的区域为{(a,b)|0≤a≤3,0≤b≤2,a≥b},
其面积为

,
所以
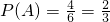
(10分)
分析:记事件A=“方程x
2+2ax+b
2=0有实根”.由△=(2a)
2-4b
2≥0,得:a
2≥b
2,当a≥0,b≥0时,方程x
2+2ax+b
2=0有实根?a≥b.
(1)基本事件共6×6=36个,其中事件A包含21个基本事件,由此能求出方程有实根的概率.
(2)全部结果所构成的区域为{(a,b)|0≤a≤3,0≤b≤2},其面积为S=3×2=6,又构成事件A的区域为{(a,b)|0≤a≤3,0≤b≤2,a≥b},其面积为

,由此能求出方程有实根的概率.
点评:本题考查古典概率及其运算公式,解题时要认真审题,仔细解答,注意合理地进行等价转化.

 (6分)
(6分) ,
,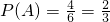 (10分)
(10分) ,由此能求出方程有实根的概率.
,由此能求出方程有实根的概率.
