
【题目】某校团委对“学生性别与中学生追星是否有关”作了一次调查,利用![]() 列联表,由计算得
列联表,由计算得![]() ,参照下表:
,参照下表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
得到正确结论是( )
A. 有99%以上的把握认为“学生性别与中学生追星无关”
B. 有99%以上的把握认为“学生性别与中学生追星有关”
C. 在犯错误的概率不超过0.5%的前提下,认为“学生性别与中学生追星无关”
D. 在犯错误的概率不超过0.5%的前提下,认为“学生性别与中学生追星有关”
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】作为加班拍档、创业伴侣、春运神器,曾几何时,方便面是我们生活中重要的“朋友”,然而这种景象却在近![]() 年出现了戏剧性的逆转.统计显示.2011年之前,方便面销量在中国连续
年出现了戏剧性的逆转.统计显示.2011年之前,方便面销量在中国连续![]() 年保持两位数增长,2013年的年销量更是创下
年保持两位数增长,2013年的年销量更是创下![]() 亿包的辉煌战绩;但2013年以来,方便面销量却连续3年下跌,只剩
亿包的辉煌战绩;但2013年以来,方便面销量却连续3年下跌,只剩![]() 亿包,具体如下表.相较于方便面,网络订餐成为大家更加青睐的消费选择.近年来,网络订餐市场规模的“井喷式”增长,也充分反映了人们消费方式的变化.
亿包,具体如下表.相较于方便面,网络订餐成为大家更加青睐的消费选择.近年来,网络订餐市场规模的“井喷式”增长,也充分反映了人们消费方式的变化.
全国方便面销量情况(单位“亿包/桶)(数据来源:世界方便面协会)
年份 |
|
|
|
|
时间代号 |
|
|
|
|
年销量 |
|
|
|
|
(1)根据上表,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .用所求回归方程预测2017 年(
.用所求回归方程预测2017 年(![]() )方便面在中国的年销量;
)方便面在中国的年销量;
(2)方便面销量遭遇滑铁卢受到哪些因素影响? 中国的消费业态发生了怎样的转变? 某媒体记者随机对身边的![]() 位朋友做了一次调查,其中
位朋友做了一次调查,其中![]() 位受访者表示超过
位受访者表示超过![]() 年未吃过方便面,
年未吃过方便面,![]() 位受访者认为方便面是健康食品;而
位受访者认为方便面是健康食品;而![]() 位受访者有过网络订餐的经历,现从这
位受访者有过网络订餐的经历,现从这![]() 人中抽取
人中抽取![]() 人进行深度访谈,记
人进行深度访谈,记![]() 表示随机抽取的
表示随机抽取的![]() 人认为方便面是健康食品的人数,求随机变量
人认为方便面是健康食品的人数,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
参考公式:回归方程:![]() ,其中
,其中 ,
,![]() .
.
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年1月26日,甘肃省人民政府办公厅发布《甘肃省关于餐饮业质量安全提升工程的实施意见》,卫生部对16所大学食堂的“进货渠道合格性”和“食品安全”进行量化评估.满10分者为“安全食堂”,评分7分以下的为“待改革食堂”.评分在4分以下考虑为“取缔食堂”,所有大学食堂的评分在7~10分之间,以下表格记录了它们的评分情况:

(1)现从16所大学食堂中随机抽取3个,求至多有1个评分不低于9分的概率;
(2)以这16所大学食堂评分数据估计大学食堂的经营性质,若从全国的大学食堂任选3个,记![]() 表示抽到评分不低于9分的食堂个数,求
表示抽到评分不低于9分的食堂个数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有些事,有些人会永远留在脑海,不会忘记,不会褪色.其实没什么放不下的,只是会觉得,付出了这么多时间,却始终没有被感动......已知抛物线![]() ,且
,且![]() ,
,![]() ,
,![]() 三点中恰有两点在抛物线
三点中恰有两点在抛物线![]() 上,另一点是抛物线
上,另一点是抛物线![]() 的焦点.
的焦点.
(1)求证:![]() 、
、![]() 、
、![]() 三点共线;
三点共线;
(2)若直线![]() 过抛物线
过抛物线![]() 的焦点且与抛物线
的焦点且与抛物线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,点
,点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛掷一蓝、一黄两枚质地均匀的正四面体骰子,分别观察底面上的数字.

(1)用表格表示试验的所有可能结果;
(2)列举下列事件包含的样本点:A=“两个数字相同”,B=“两个数字之和等于5”,C=“蓝色骰子的数字为2”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】班主任为了对本班学生的考试成绩进行分析,决定从本班24名女同学,18名男同学中随机抽取一个容量为7的样本进行分析.
(1)如果按照性别比例分层抽样,可以得到多少个不同的样本?(写出算式即可,不必计算出结果)
(2)如果随机抽取的7名同学的数学,物理成绩(单位:分)对应如下表:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
数学成绩 | 60 | 65 | 70 | 75 | 85 | 87 | 90 |
物理成绩 | 70 | 77 | 80 | 85 | 90 | 86 | 93 |
①若规定85分以上(包括85分)为优秀,从这7名同学中抽取3名同学,记3名同学中数学和物理成绩均为优秀的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
②根据上表数据,求物理成绩![]() 关于数学成绩
关于数学成绩![]() 的线性回归方程(系数精确到0.01);若班上某位同学的数学成绩为96分,预测该同学的物理成绩为多少分?
的线性回归方程(系数精确到0.01);若班上某位同学的数学成绩为96分,预测该同学的物理成绩为多少分?
附:线性回归方程![]() ,
,
其中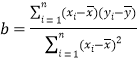 ,
,![]() .
.
|
|
|
|
76 | 83 | 812 | 526 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知函数y=4cos2x-4![]() sinxcosx-1(x∈R).
sinxcosx-1(x∈R).
(1)求出函数的最小正周期;
(2)求出函数的最大值及其相对应的x值;
(3)求出函数的单调增区间;
(4)求出函数的对称轴.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com