
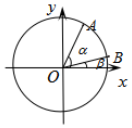
 如图,在平面直角坐标系xOy中,以x轴为始边作两个锐角α,β,它们的终边分别与单位圆交于A,B两点.已知$A(\frac{{\sqrt{5}}}{5},\;\frac{{2\sqrt{5}}}{5})\;,\;\;B(\frac{{7\sqrt{2}}}{10},\;\frac{{\sqrt{2}}}{10})$
如图,在平面直角坐标系xOy中,以x轴为始边作两个锐角α,β,它们的终边分别与单位圆交于A,B两点.已知$A(\frac{{\sqrt{5}}}{5},\;\frac{{2\sqrt{5}}}{5})\;,\;\;B(\frac{{7\sqrt{2}}}{10},\;\frac{{\sqrt{2}}}{10})$分析 (1)先求出两个锐角α,β的余弦,正弦函数值,进而利用商数关系得到两角的正切值,代入正切的和角公式求值.
(2)用正切的二倍角公式,和角公式求出2α+β的正切,再根据其正切值求2α+β的值,在确定其值前要先确定2α+β的取值范围.
解答 解:(1)由已知得:$cosα=\frac{{\sqrt{5}}}{5},cosβ=\frac{{7\sqrt{2}}}{10}$.$sinα=\frac{{2\sqrt{5}}}{5},sinβ=\frac{{\sqrt{2}}}{10}$.
∴$tanα=2,tanβ=\frac{1}{7}$.
∴$tan(α+β)=\frac{tanα+tanβ}{1-tanα•tanβ}=\frac{{2+\frac{1}{7}}}{{1-2×\frac{1}{7}}}=3$.
(2)∵tan2α=$\frac{2tanα}{1-ta{n}^{2}α}$=$\frac{4}{1-4}$=-$\frac{4}{3}$,
∴tan(2α+β)=$\frac{tan2α+tanβ}{1-tan2αtanβ}$=$\frac{-\frac{4}{3}+\frac{1}{7}}{1-(-\frac{4}{3})×\frac{1}{7}}$=-1.
∵α,β为锐角,
∴0<2α+β<$\frac{3π}{2}$,
∴2α+β=$\frac{3π}{4}$.
点评 本题考查两角和与差的正切函数,求解的关键是利用公式求出角的正切值,再求角.本题中涉及到了三角函数中的多个公式,变形灵活,做题时要注意转化正确.本题考查了转化化归的思想,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 7 | C. | 17 | D. | 27 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知四棱锥P-ABCD,底面ABCD是∠A=60°、边长为a的菱形,又PD⊥底面 ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.
已知四棱锥P-ABCD,底面ABCD是∠A=60°、边长为a的菱形,又PD⊥底面 ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知△ABD和△BCD是两个直角三角形,∠BAD=∠BDC=$\frac{π}{2}$,E、F分别是边AB、AD的中点,现将△ABD沿BD边折起到A1BD的位置,如图所示,使平面A1BD⊥平面BCD.
已知△ABD和△BCD是两个直角三角形,∠BAD=∠BDC=$\frac{π}{2}$,E、F分别是边AB、AD的中点,现将△ABD沿BD边折起到A1BD的位置,如图所示,使平面A1BD⊥平面BCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com